Question

Дана функция f (x) = x^2 - 6x - 7
а) Запишите уравнение оси симметрии графика данной функции.
б) В какой точки данной функции пересекает ось ОХ?
в) Найдите точки пересечения графика функции с осью OY.
г) Постройте график функции

Answer 1

f(x)=x²-6x-7 парабола

а) уравнение оси симметрии к для параболы имеет вид:

$x=-\frac{b}{2a}$

Т.е. ось симметрии параболы  - это прямая, проходящая через вершину параболы и параллельная ось ординат.

Для заданной функции:

a=1 b=-6

$x=-\frac{-6}{2}=3$

x=3 уравнение оси симметрии

б) График пересекает ось ОХ, при f(x)=0

x²-6x-7=0

D=6²+4*7=64=8²

x₁=(6+8)/2=7

x₂=(6-8)/2=-1

Значит график пересекает ось ОХ в точках (7; 0) и (-1; 0)

в) Функция пересекает график ОУ при х=0

f(0)=0-6*0-7=-7

(0; -7)

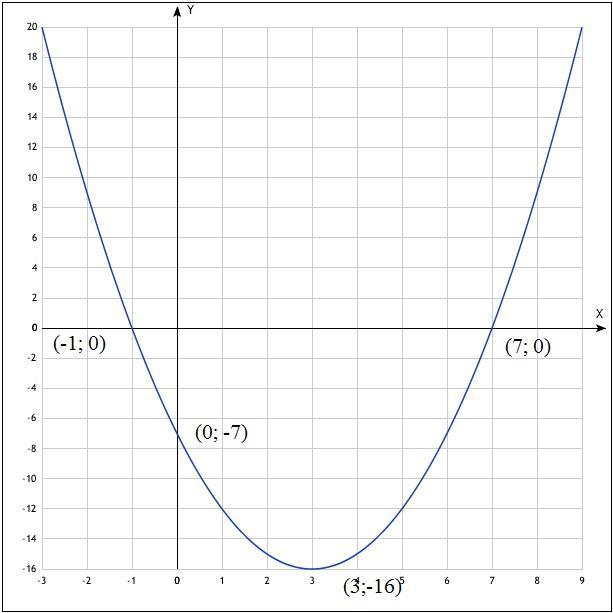
г) Построим параболу.

a>0 ветви направлены вверх

Вершина параболы:

х₀=3

y₀=9-18-7=-16