Question

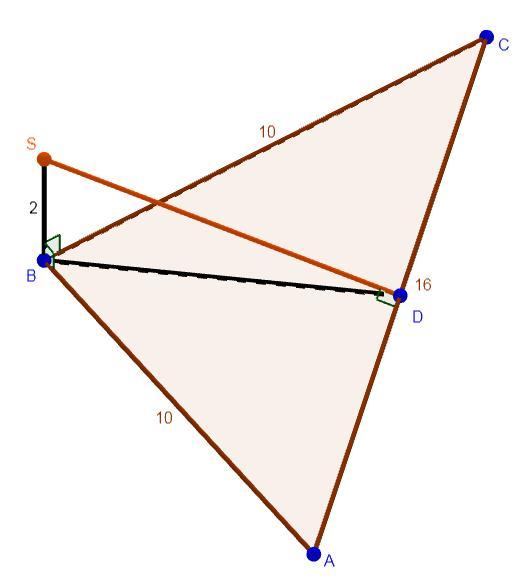
Из пункта S к плоскости равнобедренного треугольника проведен перпендикуляр SB длинной 2 см. Найти расстояние от точки S до стороны AC, если известно, что AB=BC=10cм, AC=16cм!

Answer 1

Ответ:

2√10 см

Пошаговое объяснение:

Проведем SD⊥AC, тогда по теореме о трех перпендикулярах BD⊥AC. SD — искомое расстояние.

Так как BD – высота, то BD – медиана ( ∆ABC — равнобедренный, AB=BC=10 см), поэтому AD=16/2=8см. По теореме Пифагора в ∆ABK :

$BD= \sqrt{AB^2-AD^2}=\sqrt{10^2-8^2}=\sqrt{100-64}=\sqrt{36}=6$

Аналогично в ∆SDB:

$SD= \sqrt{BD^2+SB^2}=\sqrt{6^2+2^2}=\sqrt{36+4}=\sqrt{40}=\sqrt{4}\cdot\sqrt{10}=2\sqrt{10}$