Предмет: Алгебра,
автор: leraakhnina2006
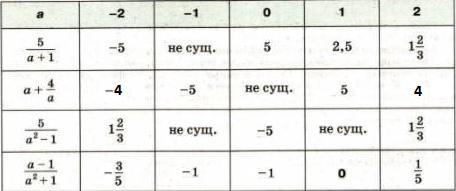
ЗАПОЛНИТЕ ТАБЛИЦУ!!ОЧЕЕЬ СРОЧНО!НАПИСАТЬ ВСЁ С ОБЬЯСНЕНИЕМ!ДАЮ 48 БАЛЛОВ!!
Приложения:

Ответы
Автор ответа:
1
Решение во вложении:
Приложения:

Автор ответа:
1
Ответ:
Таблица во вложении
Объяснение:
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: віталік25
Предмет: Русский язык,
автор: AllisonArgent
Предмет: Русский язык,
автор: stomovt
Предмет: Физика,
автор: Dayn228Debil
Предмет: История,
автор: Кошечкамария1