Предмет: Математика,
автор: ira33300
204.
Помогитеее!!!!!
Приложения:
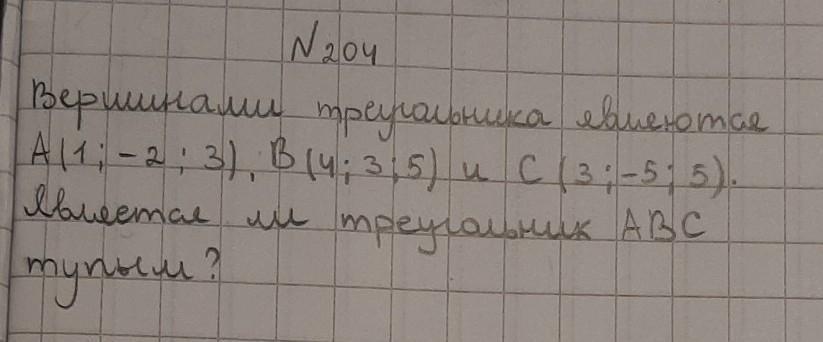
Ответы
Автор ответа:
1
Рассмотрим вектора АВ и АС и найдем косинус угла между ними.
Косинус угла между двумя векторами определяется по формуле:
Получившийся косинус отрицателен, поэтому соответствующий угол (угол ВАС) тупой. Треугольник является тупоугольным.
Похожие вопросы
Предмет: Русский язык,
автор: tnt89
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: 0004556189
Предмет: Литература,
автор: Lina674
Предмет: Математика,
автор: Lolazal99