Предмет: Математика,
автор: ira33300
207.
Помогитеее!!!!!
Приложения:
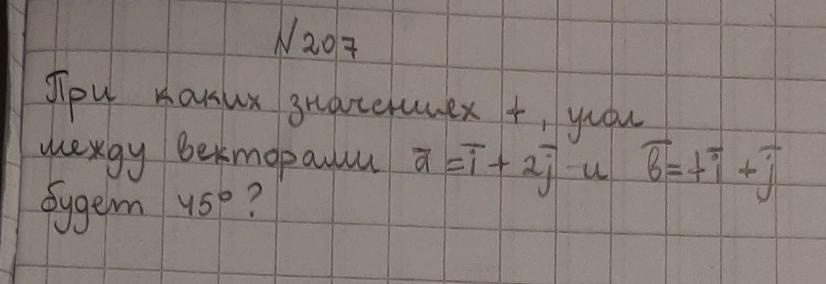
Ответы
Автор ответа:
2
Косинус угла между двумя векторами и
определяется по формуле:
Косинус 45 градусов равен . Приравняем значения:
Отметим ОДЗ:
Возведем уравнение в квадрат:
Ответ: 3 и -1/3
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Таня11111111
Предмет: Русский язык,
автор: валяс
Предмет: Математика,
автор: Влад139111
Предмет: Математика,
автор: Danya361