Question

В равнобедренной трапеции диагональ перпендикулярна боковой стороне.
Найдите площадь трапеции,если большее основание равно 12√3,а один из углов трапеции 60°

Answer 1

Ответ:

81√3 ед²

Объяснение:

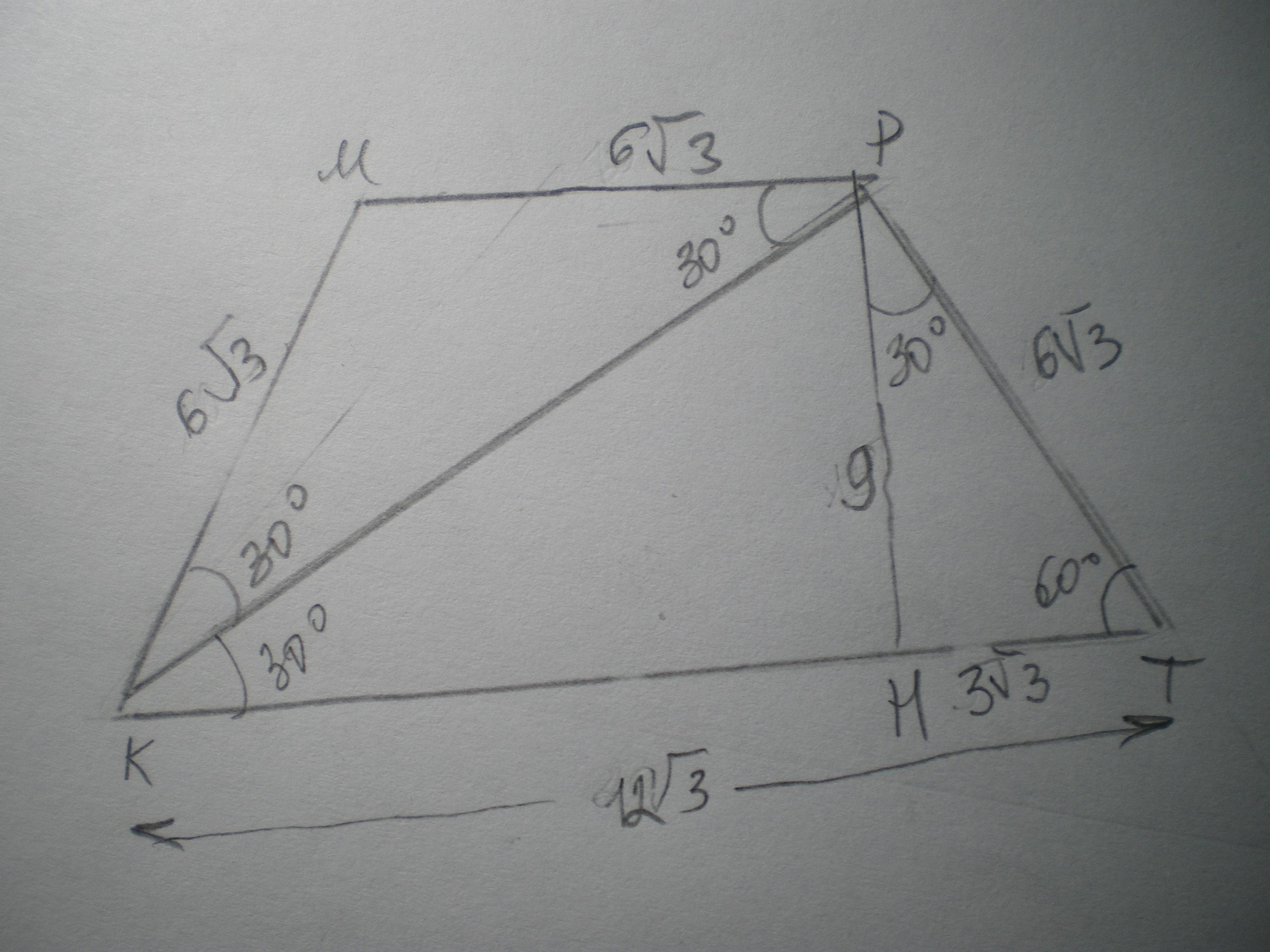
Дано: КМРТ - трапеция, КМ=РТ, ∠Т=60°,  КР⊥РТ;  КТ=12√3. Найти S(КМРТ).

Рассмотрим ΔКРТ - прямоугольный;  ∠РКТ=90-60=30°, значит, РТ=0,5КТ=6√3 по свойству катета, лежащего против угла 30 градусов.

Проведем высоту РН и рассмотрим ΔРТН - прямоугольный;

∠ТРН=90-60=30°, значит, ТН=0,5РТ=3√3.

Найдем РН по теореме Пифагора:

РН²=РТ²-ТН²=108-27=81;  РН=9.

Найдем МР.  ∠МРК=∠РКН=30° как внутренние накрест лежащие при МР║КТ и секущей КР;  ∠МКР=60-30=30°, значит, ΔКМР - равнобедренный, МР=КМ=6√3.

S(КМРТ)=(МР+КТ)/2 * РН = (6√3+12√3)/2 * 9=(9√3)*9=81√3 ед²