Предмет: Математика,
автор: Express0
Алгебра.
2.Решите в целых числах уравнение: x^2 + 1974 = y^2 или докажите, что уравнение целых решений не имеет.
Точный ответ пожалуйста)
Приложения:
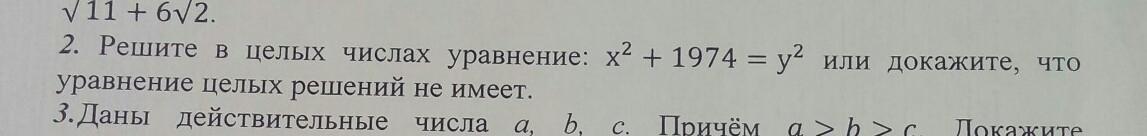
Ответы
Автор ответа:
3
Решение:
Понятно, что если - целое число, то оно может быть либо четным, либо нечетным. Рассмотрим оба случая.
1). - четное число. Тогда
- тоже четное.
Теперь пусть и
(причем
).
Подставляем:
Получается, что левая часть делится на , а правая - нет. Противоречие. Следовательно, такой случай невозможен.
2). Теперь пусть - нечетное. Тогда
такой же четности.
Опять же, и
.
При подстановке получаем:
Тот же самый парадокс - левая часть делится на , а првая - нет.
Как видим, ни тот, ни другой случай не имеют места быть. Следовательно, у уравнения нет целых решений.
Задача решена!
Ответ: ∅.
Похожие вопросы
Предмет: Українська мова,
автор: roka
Предмет: Русский язык,
автор: 87779711095
Предмет: Українська мова,
автор: roka
Предмет: Математика,
автор: Данила0411
Предмет: Музыка,
автор: Киллер11111111