Question

Построить пораболу y=4x^2+4x-3
Указать вершины и какие коодрдинаты(х,у) берутся для построения графика.

Answer 1

Ответ:

Пошаговое объяснение:

1) рассмотрим основные свойства функции типа y(x)=ax^2+bx+c в данном случае:

(1) так как при x^2  a = 4, 4>0 => у графика парабола "ветви" направленны вверх

(2) найдем x(вершины) по формуле -b/2a:

-4/8 = -1/2

(3) найдем  y(вершины) подставив x(вершины) в исходное уравнение:

y(-1/2)= 4/4 + (-4/2) - 3 = 1 - 2 - 3 = -4 => координаты вершины = C (-1/2;-4)

(4) найдем пересечения с осью OX, тоесть корни ур-ия:

Дискриминант = b^2 - 4ac = 16 + 48 = 64

x(1;2)= (-b±√дискриминант)/2a =(-4 ± √64)/8 => x(1)= (-4 + 8)/8 = 1/2 = 0,5

                                                                               x(2)= (-4-8)/8 = -12/8 = -1,5

слеедовательно координаты точек пересечения оси OX =  A (-1,5;0) и D (0,5;0)

(5) функция пересечет ось ординат OY когда х=0. Найдем координату пересечения ординаты подставив х=0 в исходное ур-ие:

y(0)= -3 => координата точки пересечения оси OY = B (0;-3)

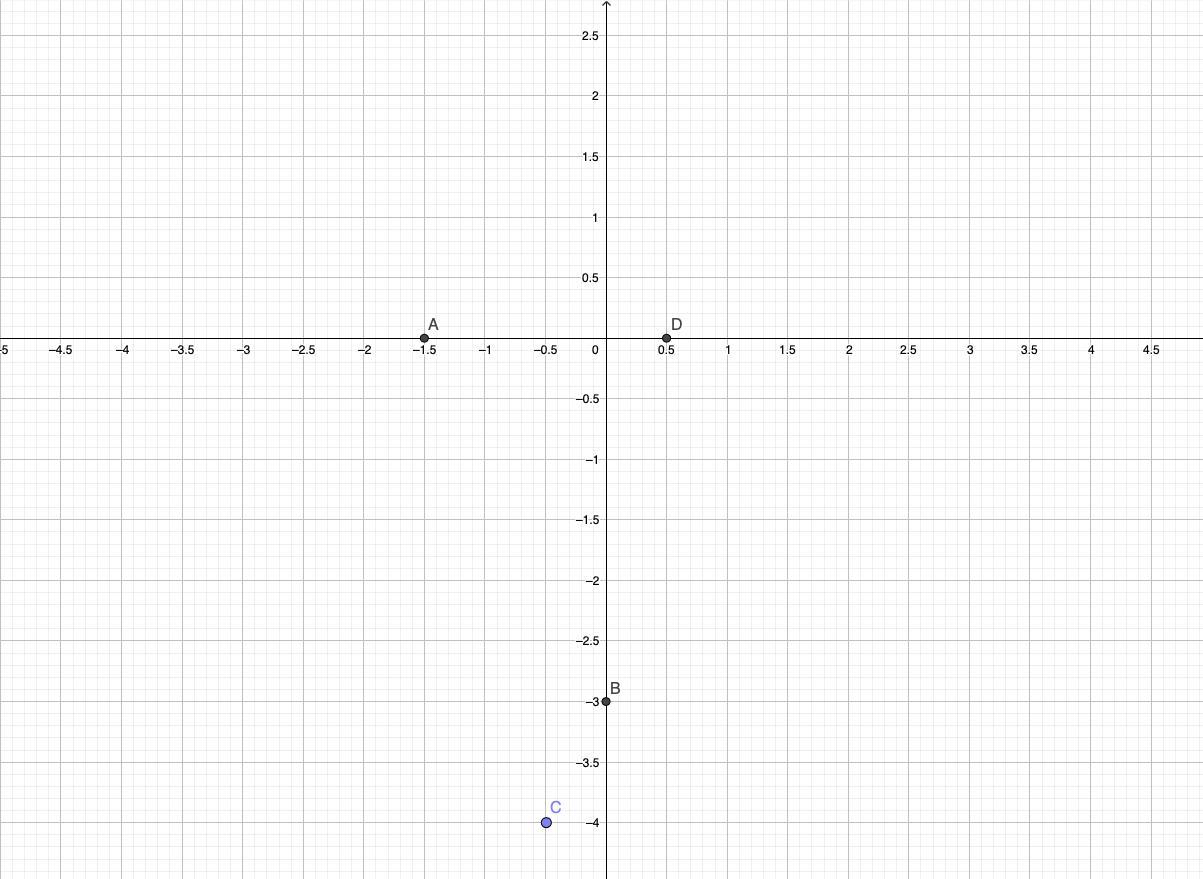
(6) мы имеем четыре точки, принадлежащие уравнению  y=4x^2+4x-3 (см рис.1)

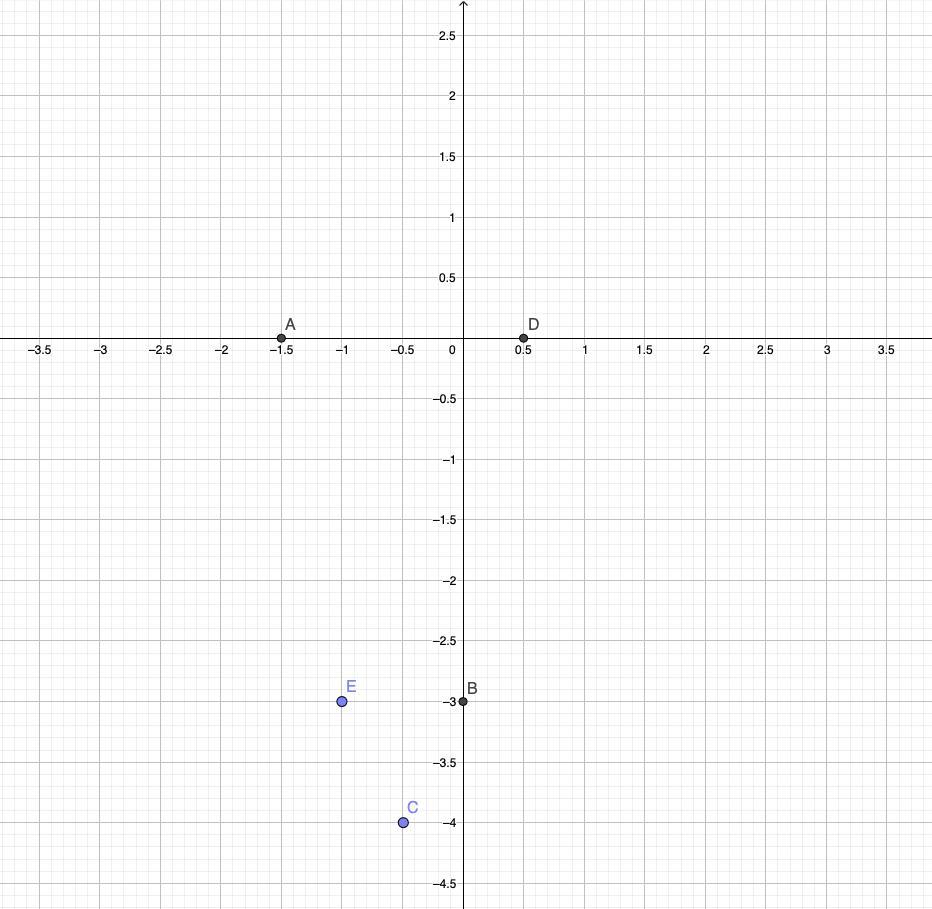
так как в график параболы полностью семетричен => точка E будет иметь одинаковую координату Y c точкой B, и симитричную координату X: E (-1;-3) (см рис.2)

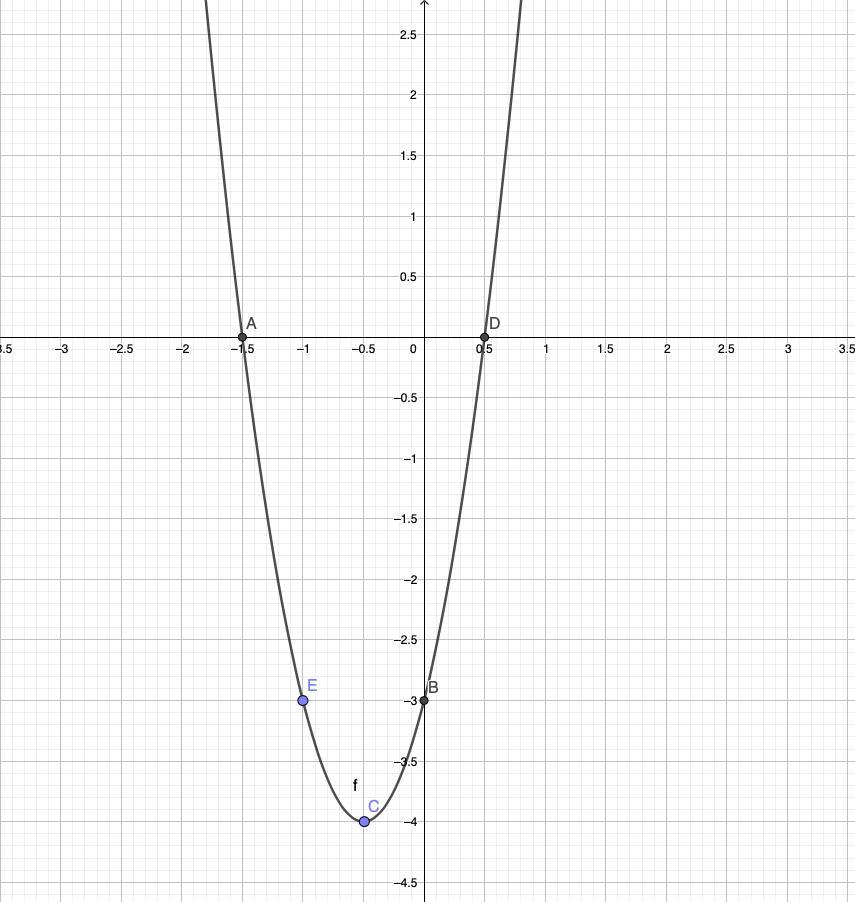
(7) соединяем точки и получаем график уравнения y=4x^2+4x-3 (см рис.3)