Предмет: Алгебра,
автор: NormickMcCormick
Логарифмическое неравенство 6
Приложения:
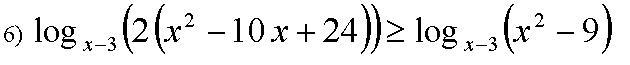
NormickMcCormick:
У меня в профиле есть ещё похожие задания, помогите с ними тоже, пожалуйста.
Ответы
Автор ответа:
0
ОДЗ:
x∈(3;4)U(6;+∞)
Можно рассмотреть два случая, когда основание
0<x-3<1
функция убывает и тогда
2(x²-10x+24)≤x^2-9
и
возрастает
{x-3>1
{2(x²-10x+24)≥x^2-9
Эти две системы методом рационализации логарифмических неравенств легко объединить в одно неравенство c cохранением знака неравенства:
(x-3-1)·(2(x^2-10x+24)-(x²-9))≥0
(x-4)·(x²-20x+57)≥0
D=400-4·57=172=4·43
x∈(5-sqrt(43);4) U (5+sqrt(43);+∞)
С учетом ОДЗ:
о т в е т. (3;4) U (5+sqrt(43);+∞)
Похожие вопросы
Предмет: Русский язык,
автор: лама1234
Предмет: Русский язык,
автор: ЮлёкКотова
Предмет: Русский язык,
автор: fortoona
Предмет: Математика,
автор: salabon1998
Предмет: Алгебра,
автор: frog9902