Предмет: Алгебра,
автор: NormickMcCormick
Логарифмическое неравенство номер 7
Приложения:
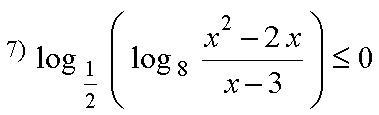
NormickMcCormick:
У меня в профиле есть ещё задания, помогите с ними тоже, пожалуйста.
Они похожи.
Ответы
Автор ответа:
0
Выражение под знаком логарифма не может быть отрицательным и
логарифмическая функция с основанием (1/2) убывающая, поэтому
получаем систему двух неравенств:
Второе неравенство сильнее первого, остается только оно
(например в системе t>0 и t ≥1 решение t≥1):
Решаем методом интервалов:
__-__ (3) __+_ [4] __-__ [6] __+__
О т в е т. (3;4] U [6;+∞)
Похожие вопросы
Предмет: Другие предметы,
автор: olesiaserova
Предмет: Другие предметы,
автор: jeni678
Предмет: Русский язык,
автор: qwerfdsa1
Предмет: Математика,
автор: Agasira20
Предмет: Математика,
автор: nika78905