Предмет: Алгебра,
автор: ghazaryangreta1467
Пожалуйста помогите
Приложения:
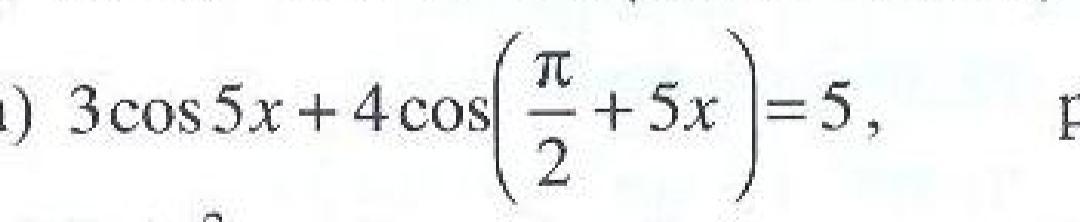
Ответы
Автор ответа:
1
cos((π/2)+5x)=-sin5x
3cos5x-4sin5x=5
Уравнение решают методом введения вспомогательного угла:
Делим обе части уравнения на √3²+(-4)²=√25=5
(3/5) сos5x-(4/5)sin5x=1
Вводим вспомогательный угол φ:
cosφ=3/5
sinφ=4/5
откуда
φ = arcsin(4/5) = arccos(3/5)
(sin²φ+cos²φ=1, так как (3/5)²+(4/5)²=1 - верно)
Получим:
сosφ· сos5x- sinφ·sin5x=1
Применяем формулу косинуса суммы:
cos(5x+φ)=1
5x+φ=2πn, n ∈Z
5x=-φ+2πn, n∈Z
5x=-arccos(3/5)+2πn, n∈Z
x=-(1/5)arccos(3/5)+(2/5)πn, n∈Z - о т в е т.
Похожие вопросы
Предмет: Русский язык,
автор: DarkLordanus
Предмет: Русский язык,
автор: Quertesa
Предмет: Русский язык,
автор: 129088
Предмет: Алгебра,
автор: Vovan4ik1777
Предмет: История,
автор: qwertyzxc3