Предмет: Алгебра,
автор: lyanova1
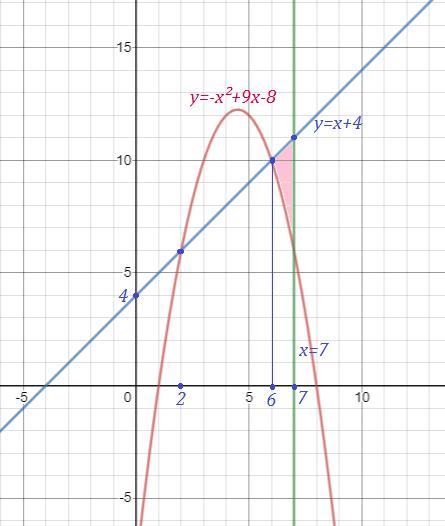
Вычислить площади фигуры,ограниченной графиками функции
у=-x^2+9x-8, y=x+4, x=7
Ответы
Автор ответа:
1
Точки пересечения параболы и прямой:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Анкоу
Предмет: Русский язык,
автор: Alina1501
Предмет: Українська мова,
автор: IrushkaDiki
Предмет: Математика,
автор: супермен30001
Предмет: История,
автор: kamillacatcat