Предмет: Алгебра,
автор: teaelite
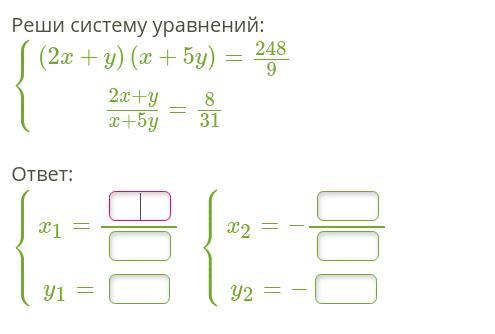
Даю 30 баллов! Прошу помочь решить систему уравнений.
Приложения:
Ответы
Автор ответа:
2
Ответ:
Решение:
Похожие вопросы
Предмет: Русский язык,
автор: demidovdima
Предмет: Английский язык,
автор: Терри111
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: матем127