Предмет: Алгебра,
автор: pochemynet
Докажите неравенство
Приложения:
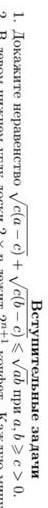
Ответы
Автор ответа:
1
Пусть некоторая тройка - решение, т.е. удовлетворяет неравенству. Тогда легко проверить, что любая тройка
тоже подходит. Выберем
. Перепишем наше неравенство:
. После увеличения каждой переменной в указанное количество раз, получим:
.
Итого: . Теперь можем оценить левую часть, используя нер-во между ср.арифм. и ср.геом.:
, что и требовалось
Похожие вопросы
Предмет: Русский язык,
автор: Olgapogrebnyak
Предмет: Русский язык,
автор: Katunay
Предмет: Русский язык,
автор: lena1984
Предмет: Литература,
автор: npi27218
Предмет: Математика,
автор: Naima1111