Question

прямоугольном треугольнике один из острых углов в 2 раза больше другого Найдите его большую сторону если, меньшая равна 6 см​

Answer 1

Дано:

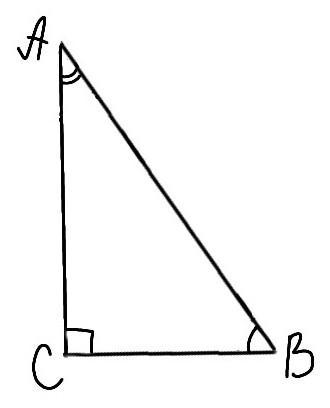
∆АВС – прямоугольный

∠В=2×∠А

СВ=6см

Найти:

АС

Решение:

Пусть ∠А – х, тогда ∠В – 2х

Составим уравнение:

х+2х=90 (т.к. сумма острых углов прямоугольного треугольника равна 90°)

3х=90

х=90÷3=30

Значит, ∠А=30°

Из этого следует, что СВ=1/2АВ

АВ=СВ×2=6×2=12см

АВ²=СВ²+АС²

12²=6²+АС²

144=36+АС²

АС²=144-36=108

АС=√108см=6√3см

Ответ: АС=6√3см.

Answer 2

Ответ:

Объяснение:

x+2x=90°

3x=90°

x=90°÷3

x=30°  <1

<2=2×30°=60°

6/sin 30°= x/sin 60°

x=6×sin 60° / sin 30° = 6 ×√3/2 /  1/2 = 3√3 ÷ 1/2 =3√3×2=6√3 см​