Предмет: Математика,
автор: dyum29
Решите неравенство, Егэ
Приложения:
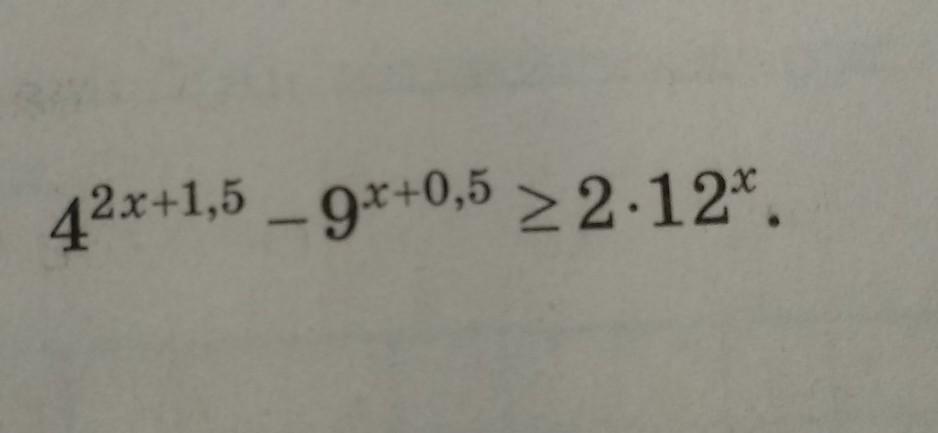
Ответы
Автор ответа:
1
Заменим (4/3)^x = t, t > 0. Тогда наше неравенство будет выглядеть:
Так как на переменную t стоит ограничение t > 0, а -1/2 не входит в этот промежуток, то решением неравенства относительно t является промежуток [3/4;+∞) или t ≥ 3/4.
Проводим обратную замену:
Ответ:
s0807:
t > 3/4 тут больше равно?
да, не заметил)
Похожие вопросы
Предмет: Русский язык,
автор: масянянька
Предмет: Русский язык,
автор: breathless
Предмет: Русский язык,
автор: erkewa98
Предмет: Математика,
автор: amantursuiunbe
Предмет: Математика,
автор: dary7