Question

решите неравенство (на фотографии)

Answer 1

Из условия следует, что

$g(x)=x^2+2x+2$. Соответственно $|g(x)-2|=|x^2+2x+2-2|=|x^2 + 2x|$ $|x|>|x^2+2x|$Решение разбиваем на два случая.

I случай: $x\leq 3$. Тогда $f(t)=t$, соответственно $f(|x|)=|x|$.

В этом случае неравенство принимает следующий вид:

$|x|>|x^2+2x|\Leftrightarrow (x-(x^2+2x))(x+(x^2+2x))>0;\\\\(-x^2-x)(x^2+3x)>0;\\\\-x(x+1)x(x+3)>0;|:(-1)\\\\x^2(x+1)(x+3)<0$

Так как значение выражения $x^2$ - неотрицательно пр любом $x$, то оно на знак левой части влиять не будет. Поэтому (с учетом того, что $x\neq 0$) на него можно разделить обе части. В итоге имеем неравенство

$(x+1)(x+3)<0$, которое решаем методом интервалов (вложение 1) и получаем интервал $(-3; -1)$ (вложение 1) Условие $x\leq 3$ он полностью удовлетворяет, поэтому первая часть ответа получена.

2 случай: $x>3$. Тогда $f(t)=9-2t$. Соответственно$f(|x|)=9-2|x|$. В этом случае неравенство принимает следующий вид:

$9-2|x|>|x^2+2x|$

В нашем случае, так как мы рассматриваем случай, когда x > 3, оба модуля раскрываются со знаком +, поэтому в итоге имеем неравенство

$9-2x>x^2+2x;\\\\x^2+4x-9<0$

Находим нули левой части:

$D=4^2-4\cdot(-9)=16+36=52=4\cdot13;\\\\x_{1,2}=\frac{-4\pm\sqrt{4\cdot13} }{2\cdot1}=\frac{-4\pm2\sqrt{13}}{2}=-2\pm\sqrt{13}$

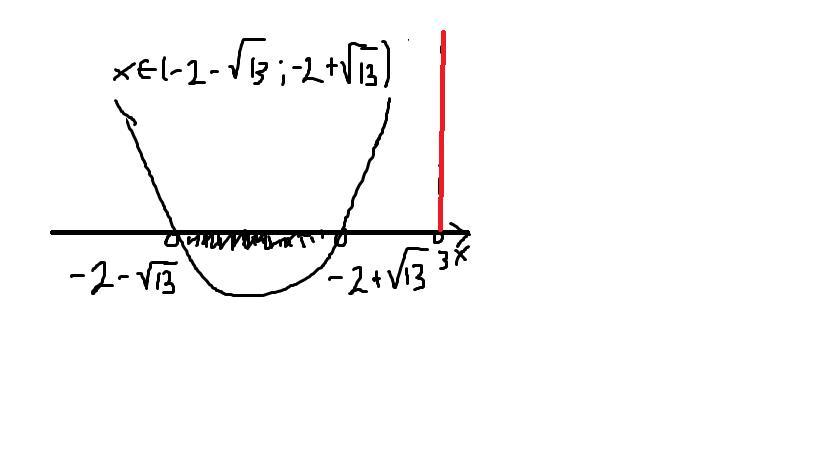
Решая неравенство методом параболы (вложение 2), получаем: $x\in (-2-\sqrt{13};-2+\sqrt{13})$. Но найденный интервал не удовлетворяет условие x > 3, поэтому в этом случае неравенство не будет иметь решений.

Значит, итоговый ответ - первый найденный интервал.

ОТВЕТ: (-3; -1).