ПОЖАЛУЙСТА ПОМОГИТЕ!!!!!!! У МЕНЯ НЕ ПОЛУЧАЕТСЯ РЕШИТЬ
Ответы
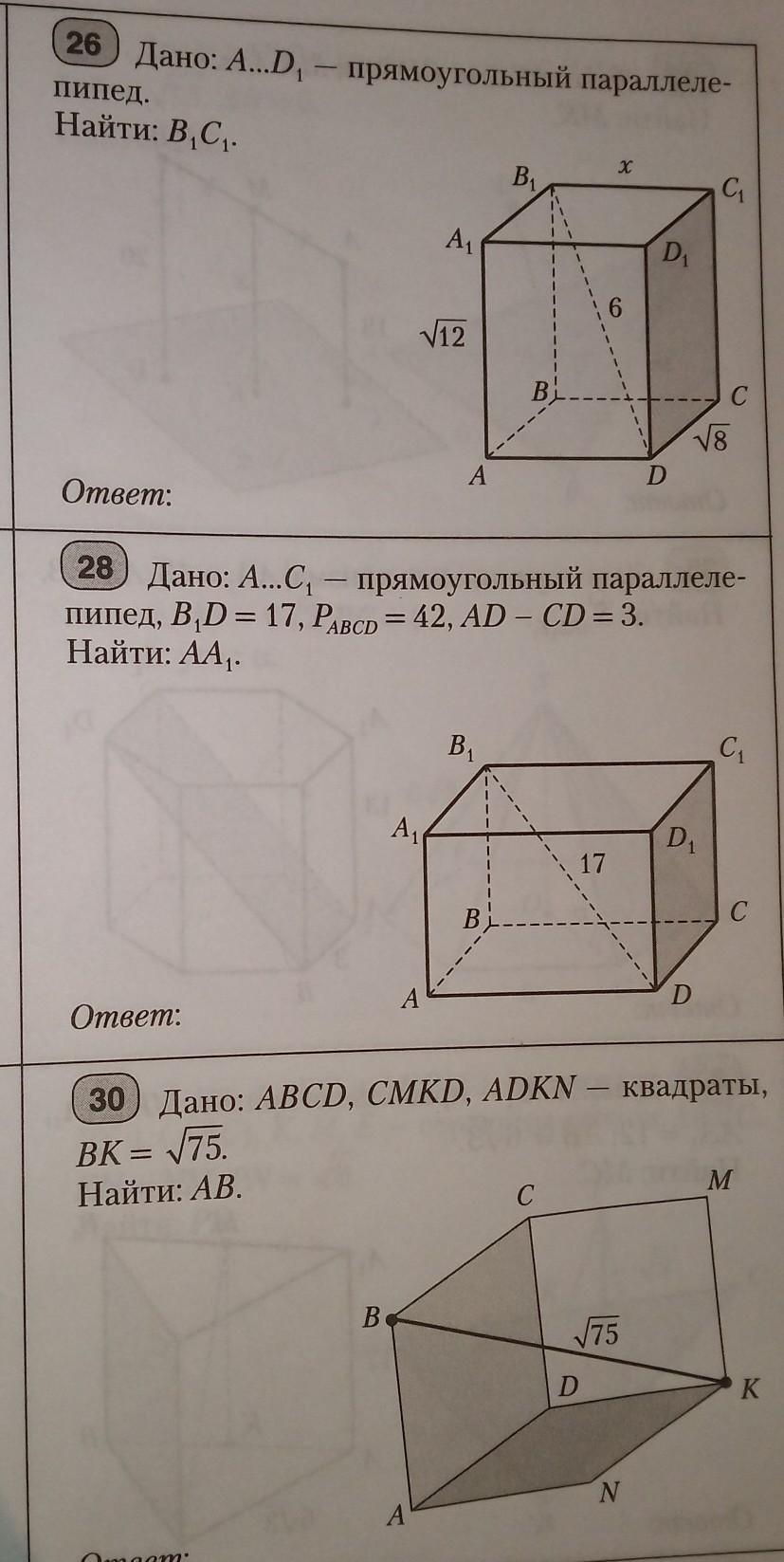
Объяснение: №26 Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений (длины, ширины, высоты), т.е. 6²= х² + (√12)² + (√8)², отсюда 36= х²+12+8, 36=х²+20, х²=16 х=4, ответ: В₁С₁= 4 №28 Так как периметр прямоугольника АВСД равен 42, то полупериметр в 2 раза меньше, т.е. АД+СД=21. По условию АД - СД=3. Сложим почленно два последние равенства, получим: АД+СД+АД - СД = 21+3 , отсюда 2· АД=24, АД=12. Значит СД=12-3=9. Используя свойство диагонали прямоугольного параллелепипеда, получим: В₁Д² =АД²+СД²+АА₁², тогда 17²=12²+9²+АА₁² 289= 144+81+АА₁², 289=225+АА₁² АА₁²=64 АА₁ = 8 Ответ: АА₁ = 8 №30 Пусть АВСД, СМКД, АДКN- квадраты со стороной а, тогда ВК - диагональ куба со стороной а (частный вид прямоуг. параллелепипеда). Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений , значит а²+а²+а²= (√75)² 3·а²=75 а²=25 а=5 Ответ: АВ=5