Предмет: Алгебра,
автор: bertain
Задание на фотографии
Приложения:

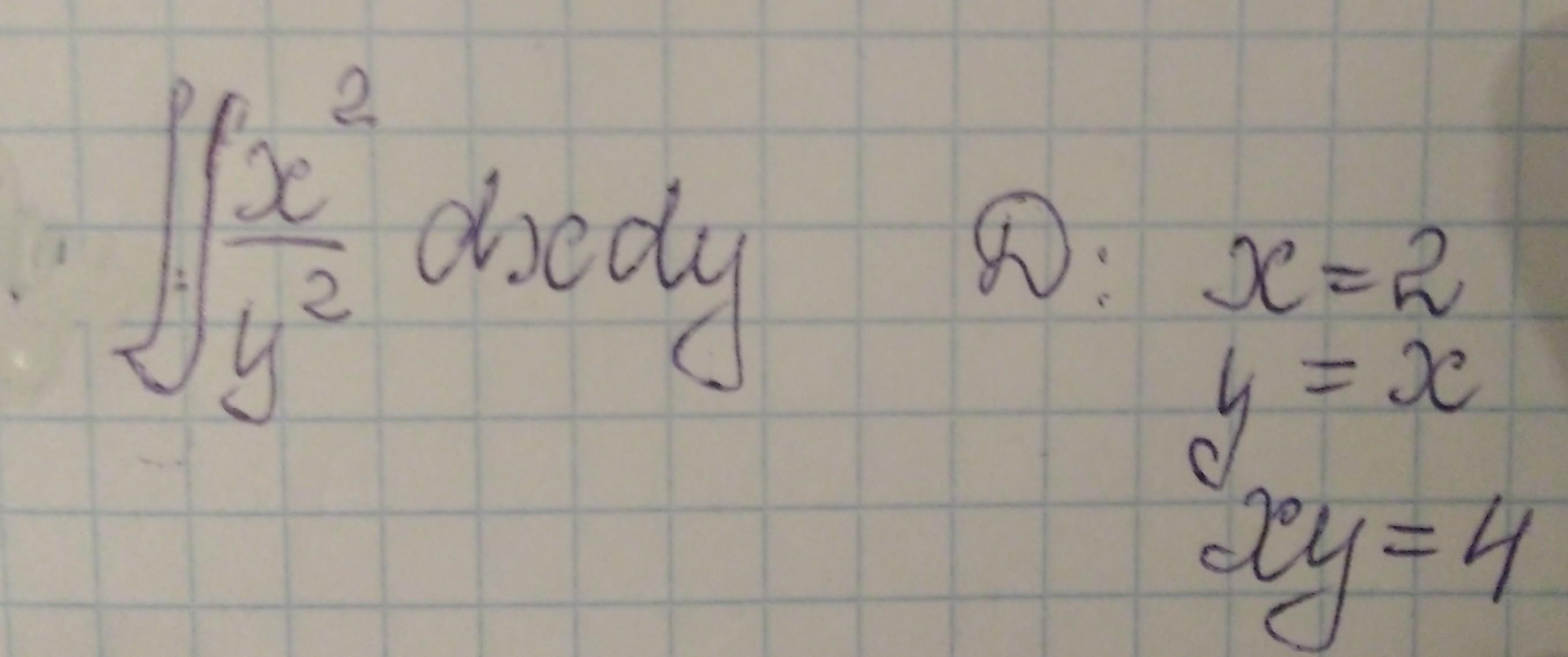
Аноним:
в подынтегральной функци y = x^2/y^2 ???
Да
А почему равно?)
случайно)) сейчас исправлю условие, спасибо, что подсказали)
Тогда всё ок )
А ответ будет? У меня вышло -1
ответов нет, к сожалению
В решении не уверен, но все же лучше чем нечего
Ответы
Автор ответа:
2
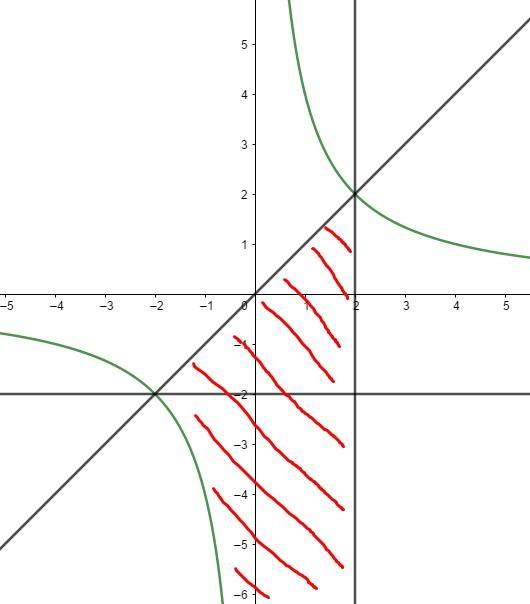
Наша область является неограниченной снизу и разобъем данную область прямой y = -2. Будем рассматривать как сумму двух интегралов
Приложения:
Автор ответа:
3
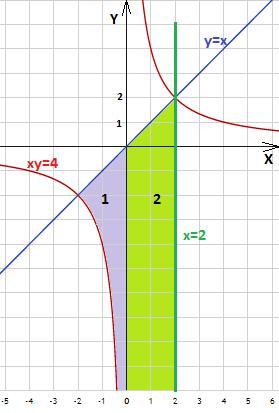
Область интегрирования можно разбить на две части :
1) x∈[-2;0) , снизу область ограничена гиперболой y = 4/x, сверху прямой y=x (на рисунке залита фиолетовым цветом )
2) x∈[0;2] , снизу область не ограничена, сверху ограничена прямой y=x (на рисунке залита зелёным цветом )
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: 123дима1
Предмет: Русский язык,
автор: Насянка
Предмет: Математика,
автор: семен71
Предмет: Биология,
автор: Ангелина1301