Question

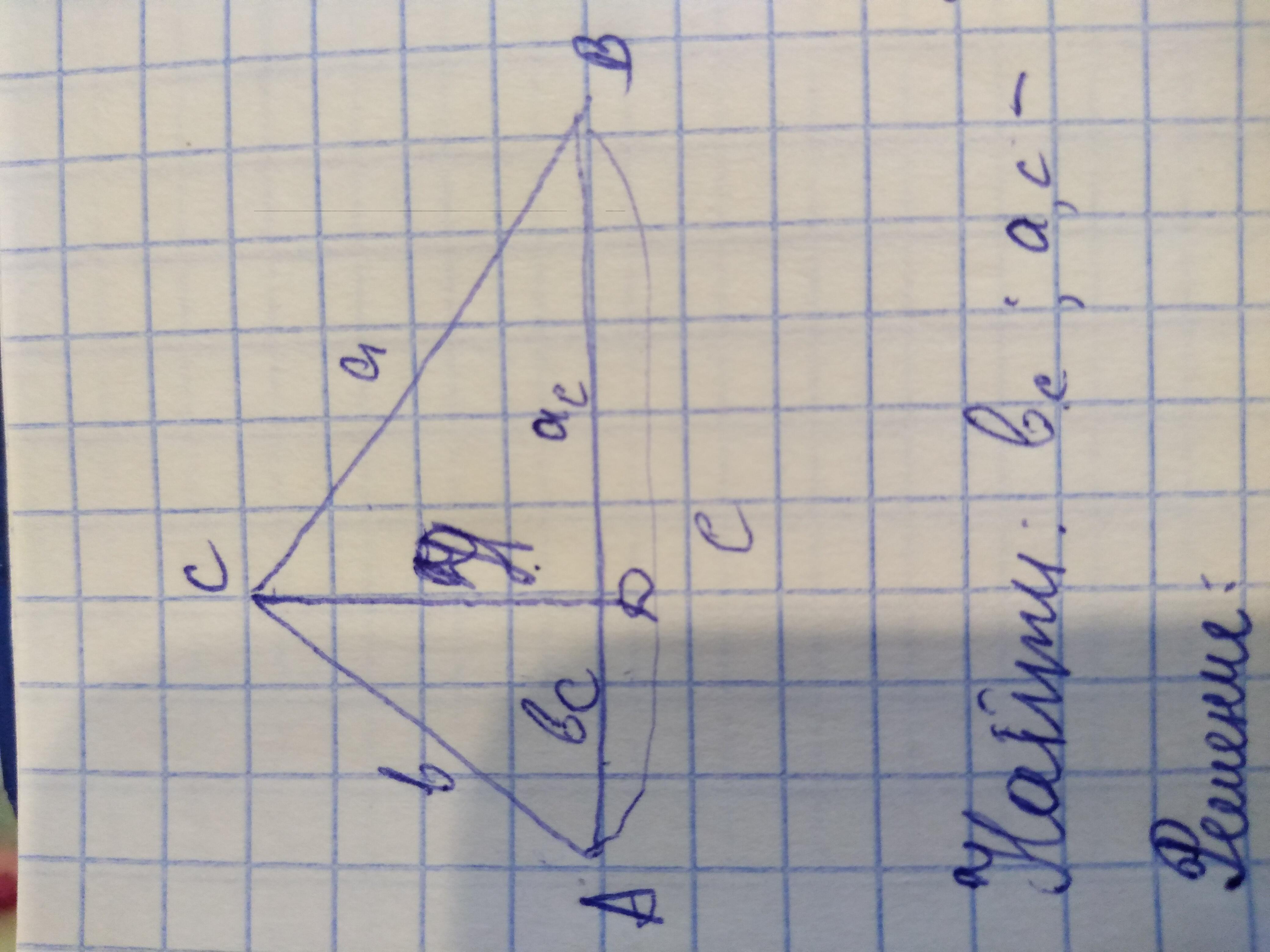
Дано треугольник АБС, угол с=90°, б=3 см,а=4 см, с=5см, СД перпендикулярно АБ. Найти бс и ас

Answer 1

с²=а²+b²

c²=3²+4²=8+16=25

c=√25=5см

b=√c×b$_{c}$

b²=c×b$_{c}$

b$_{c}$=b²÷c=3²÷5=9÷5=1,8см

а=√с×а$_{c}$

а²=с×а$_{c}$

а$_{c}$=а²÷с=4²÷5=16÷5=3,2см

Ответ: а$_{c}$=3,2см; b$_{c}$=1,8см.

Answer 2

Ответ:

bc=1.8 ac=3.2

Объяснение:

По свойствам прямоугольного треугольника высота проведенная из вершины прямого угла делит гипотенузу на отрезки, в нашем случае $b_{c}$ и $a_{c}$

и отрезки эти равны:

$b_{c} = \frac{b^{2}}{c} \\a_{c} = \frac{a^{2} }{c}$

найдём их:

$b_{c} =\frac{3^{2}}{5} = \frac{9}{5} = 1,8\\a_{c} = \frac{4^{2}}{5} = \frac{16}{5} = 3,2$