Предмет: Алгебра,
автор: pleasure123
Помогите с тригонометрией
Приложения:
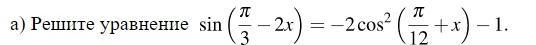
Ответы
Автор ответа:
1
Ответ:
nikebod313:
Каких-либо объяснений здесь нет. Если будет что-то не понятно,— спрашивайте.
Похожие вопросы
Предмет: Русский язык,
автор: kykla13
Предмет: Русский язык,
автор: Nastyonka25
Предмет: Русский язык,
автор: MashaNesterova
Предмет: Физика,
автор: MariaMironova