Предмет: Математика,
автор: carabaevroma
Можно подробное решение, нужно срочно . 50 баллов
Приложения:
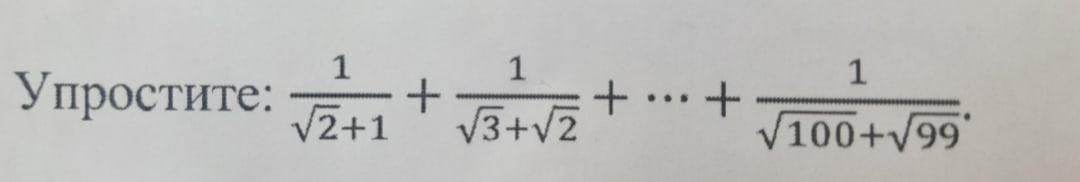
Ответы
Автор ответа:
1
Ответ:
9
Пошаговое объяснение:
Похожие вопросы
Предмет: Другие предметы,
автор: растиш
Предмет: Русский язык,
автор: Аноним
Предмет: Беларуская мова,
автор: патрицияатом
Предмет: Математика,
автор: ККК2005
Предмет: Математика,
автор: dorzhimadandarova