Question

20 баллов! Решите неравенства

Answer 1

1.

Квадратное неравенство относительно tgx

Замена переменной:  tgx=t

3t²+t-4≥0

Находим корни квадратного трехчлена:

D=1-4·3·(-4)=49

t₁=  -4/3;  t₂=1

Решение неравенства:

t≤-4/3  или   t ≥1

Обратный переход к переменной х:

tgx ≤-4/3   или   tgx ≥1

О т в е т.

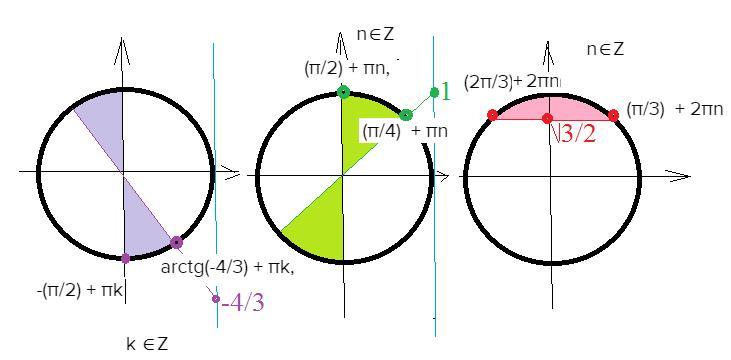
-(π/2) + πk < x≤arctg(-4/3) + πk, k ∈Z  или (π/4)  + πn ≤x < (π/2) + πn, n∈Z

2.

Так как сos²x=1-sin²x

2·(1-sin²x)-√3·sinx+1≤0

2·sin²x+√3·sinx-3≥0

Квадратное неравенство относительно sinx

Замена переменной:  sinx=t

2t²+√3t-3≥0

Находим корни квадратного трехчлена:

D=3-4·2·(-3)=27

t₁=  -√3;  t₂=√3/2

Решение неравенства:

t≤-√3  или   t ≥√3/2

Обратный переход к переменной х:

sinx < -√3 - нет решений, так как |sinx|≤1   или

sinx ≥√3/2

(π/3)  + 2πn ≤x ≤ (2π/3) + 2πn, n∈Z