Предмет: Геометрия,
автор: mragelmusic
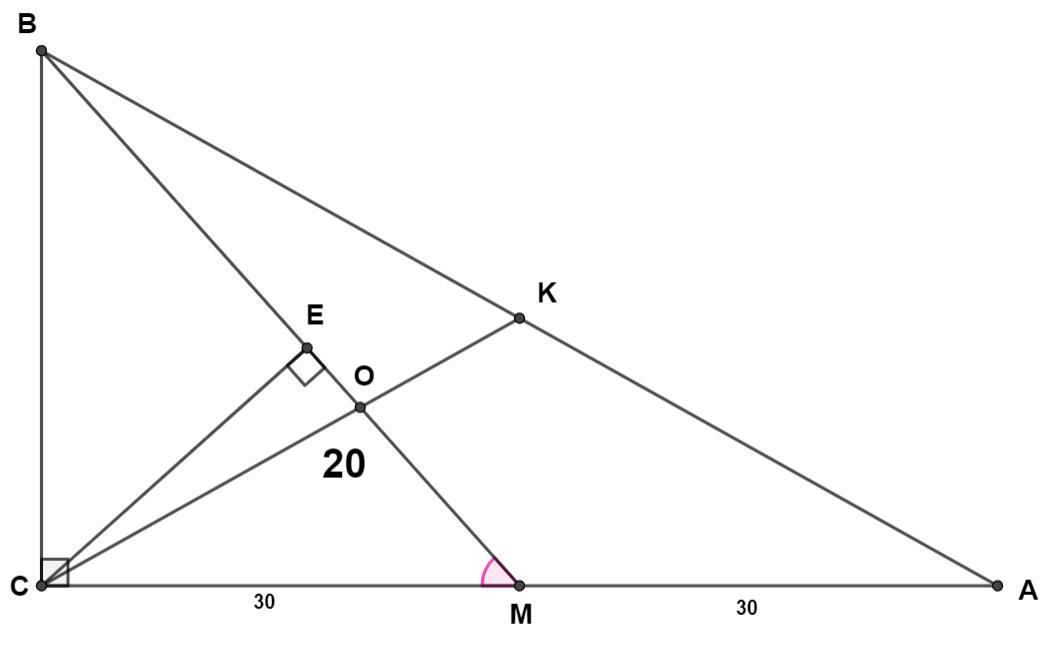
В прямоугольном треугольнике ABC (угол C = 90 гр.) медианы ВМ и СК пересекаются в точке О. Из точки С на ВМ опущен перпендикуляр СЕ так, что МЕ = 20 см. Найдите гипотенузу АВ, если МС = 30 см, точка О лежит на отрезке МЕ.
Ответы
Автор ответа:
7
ΔBCM ~ ΔCEM по двум углам (∠BCM=90°=∠CEM и ∠BMC - общий), поэтому .
Откуда BM = 900:2 = 45см
BE = BM-EM = 45-20 = 25см
В прямоугольном треугольнике CEM (∠E=90°):
по теореме Пифагора CE²=CM²-EM²=900-400=500см².
В прямоугольном треугольнике BEC (∠E=90°):
по теореме Пифагора BC²=BE²+CE²=625+500=1125см².
AC=2·MC=60см т.к. M - середина AC.
В прямоугольном треугольнике BCA (∠C=90°):
по теореме Пифагора AB²=BC²+AC²=1125+3600=4725см².
AB= см
Ответ: 15√21 см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: RedLake
Предмет: Русский язык,
автор: lednevsasha9
Предмет: Русский язык,
автор: Boss3
Предмет: Химия,
автор: Wahmurad
Предмет: Математика,
автор: LiskaKiska111