Предмет: Алгебра,
автор: darkomarco
очень срочно!!! решить логарифмическое неравенство!
Приложения:
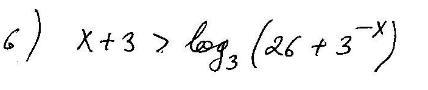
Ответы
Автор ответа:
0
Замена переменной
Метод интервалов
- не подходит, так как y > 0
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: milastr
Предмет: Русский язык,
автор: tayaredkozub
Предмет: Математика,
автор: Juuuuulih
Предмет: Физика,
автор: chashka1245