Предмет: Алгебра,
автор: paulmanjulia
Найдите наибольшее и наименьшее значения функции
 ,
,
на отрезке ![[-\frac{1}{2};2] [-\frac{1}{2};2]](https://tex.z-dn.net/?f=%5B-%5Cfrac%7B1%7D%7B2%7D%3B2%5D)
Simba2017:
а то я ухожу
Да, давайте
вас интересует их сумма
скопируйте и я удалю их
сделали копию?
минимум будет около 0 у суммы-согласны? максимум у х=2
Почему производную бесполезно? Здесь можно использовать производную функции не смотря на модульное выражение
пишите....
удаляю...
Удаляйте. А как тогда использовать производную?
Ответы
Автор ответа:
1
Область определения функции: x > 0
Рассмотрим два случая:
1) Если 0 < x < 1, то
Получаем , но рассматриваемая точка экстремума положительная, поэтому откидываем значение x = -1.
(0)__+___(1/2)____-___(1)
Вертикальная асимптота: x = 0 и учитывая то, что функция возрастает с 0(не включая) до значения x=1/2, то у функции наименьшего значения нет.
2) Если 1 < x ≤ 2, то - возрастает на промежутке x > 1. Но на промежутке x ∈ (1; 2] будет наибольшее значение функции в точке x = 2 и равно оно
. Наименьшего значения функции не существует.
Приложения:
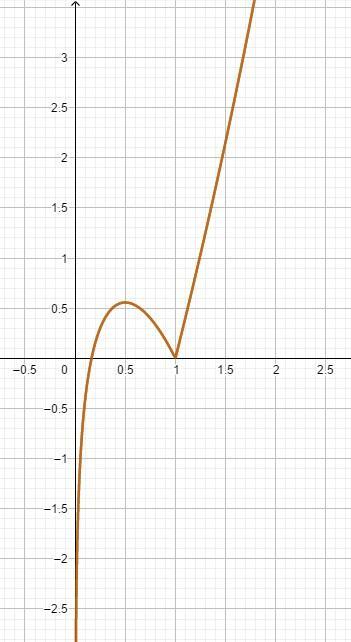
Надо проверить на счет (0;1) возрастает и убывает. Правильно сформулировать нужно
Хорошо, спасибо вам большое!
ошибки у вас...
вижу
не хотелось такое решение отмечать нарушением-напишите модератору сами-пошлю на исправлеие
Похожие вопросы
Предмет: Русский язык,
автор: Лика01
Предмет: Українська мова,
автор: DImaBychenko
Предмет: Українська мова,
автор: kittycat13
Предмет: Физика,
автор: мику02010216
Предмет: Биология,
автор: efanovvadim