Предмет: Алгебра,
автор: dimon4ikkkk
Алгебра. 9 класс.
1. Упростите выражение: cos(п-a)tg(п+a)/sin(п/2-a)
2. Вычислите:
A) cos40° cos20°- sin40° sin20°
B) sin105°
3. Упростите выражение:
A) sin2a/2ctga
B) 1-cos2a/1+cos2a
Ответы
Автор ответа:
12
Ответ:
все. ответ готов......
Приложения:

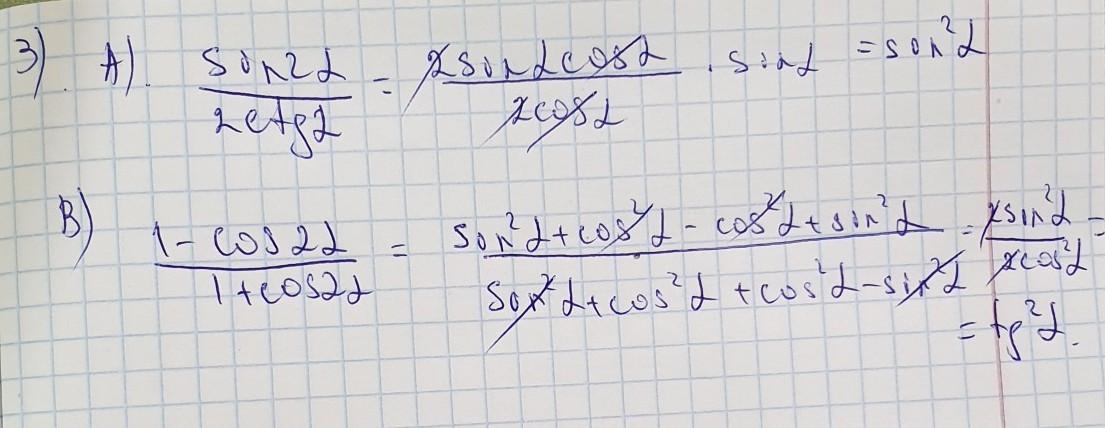
Автор ответа:
9
Похожие вопросы
Предмет: Русский язык,
автор: bukin
Предмет: Русский язык,
автор: irka424
Предмет: Английский язык,
автор: Daria0schoolgirl
Предмет: Геометрия,
автор: 12345567788999999
Предмет: Геометрия,
автор: antonova6012003