Предмет: Алгебра,
автор: shkila62
Найдите при каких значениях числа a система уравнений имеет два решения
Приложения:
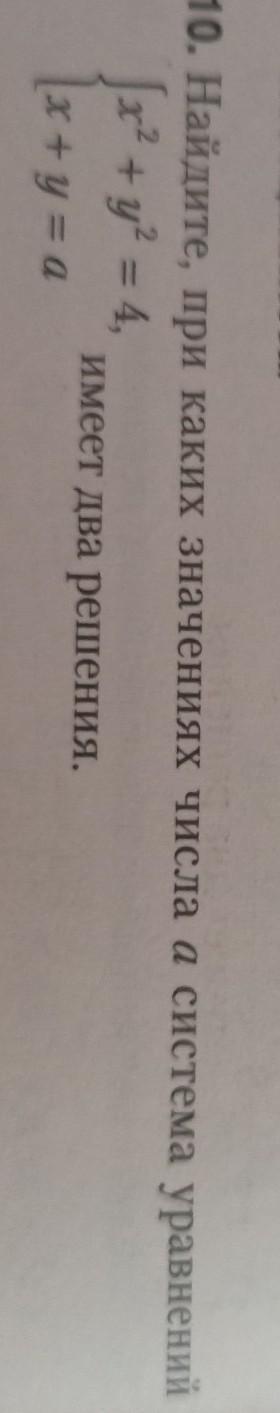
Ответы
Автор ответа:
21
Решим уравнение относительно a.
Уравнение будет иметь 2 корня, если D>0.
a∈(-2√2; 2√2)
Похожие вопросы
Предмет: Русский язык,
автор: КошкаФМ
Предмет: Русский язык,
автор: Viktoria77777
Предмет: Русский язык,
автор: стиканов
Предмет: Математика,
автор: neizvestno6