Предмет: Алгебра,
автор: kjuliyaa
100 баллов, ПРЕДЕЛЫ!!!
Решите пределы, не применяя производную!
ответы:
112: -1
107: 14
98: -2
106:-1/24
113: корень из 3
115: - корня из 2
131: 1
Приложения:
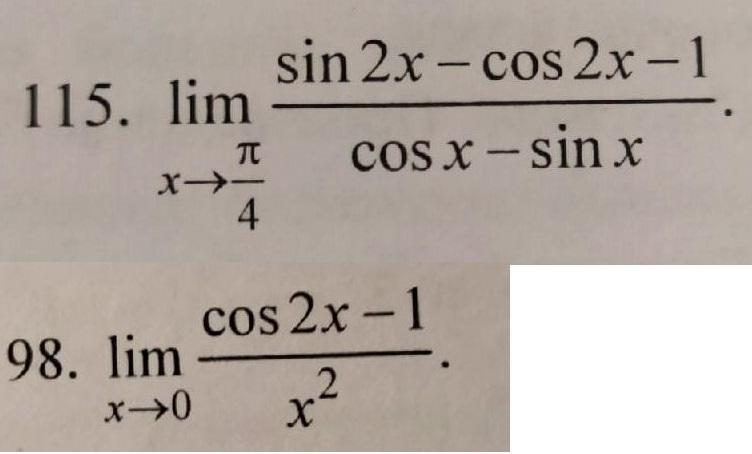


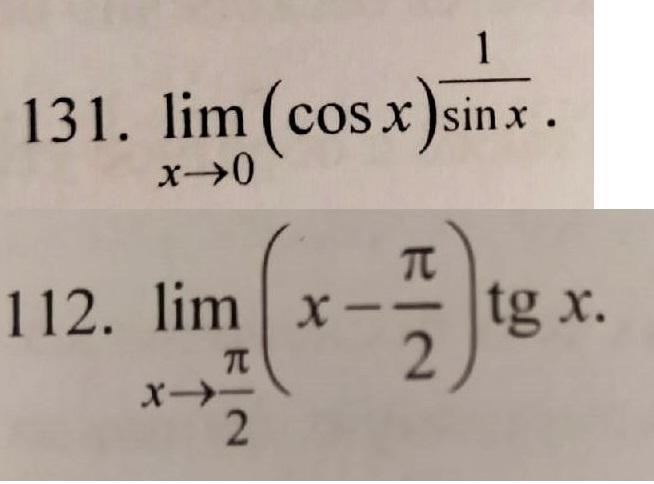
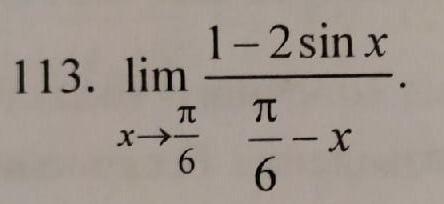
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: Katonov
Предмет: Русский язык,
автор: юльчик18
Предмет: Русский язык,
автор: ээээээхх
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Radis001