Question

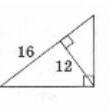
в прямоугольном треугольнике проведена высота из вершины прямого угла. найти гипотенузу(фото прикладываю)
(16 это только кусок)​ помогите пж

Answer 1

Ответ: 25

Объяснение:

Рассмотрим треугольник со сторонами 16 и 12, в нем неизвестная сторона будет равна: х=$\sqrt{16^{2}+12^{2}$=20

Воспользуемся свойством высоты в прямоугольном треугольнике, проведенной из прямого угла:

Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных ему, каждый из которых подобен данному.

Используя отношение найдем второй катет большого треугольника через маленькие:

$\frac{20}{x}=\frac{16}{12}$, где х=15

Найдем гипотенузу через формулы площади треугольника.

S=$\frac{a*h}{2}$, где а=16+х, h=12

а=16+х-гипотенуза

S=$\frac{a*b*sin\alpha }{2}$, где sin90=1, а=20, b=15.

S=$\frac{20*15}{2}$=150

150=$\frac{a*12}{2}$, а=$\frac{150*2}{12}$=25.