Предмет: Геометрия,
автор: nvmyb01
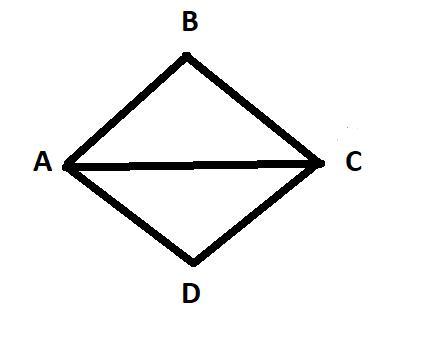
Докажите, что AB || CD и BC || AD, если AB=BC=CD=AD
Приложения:
Ответы
Автор ответа:
1
ABCD- квадрат. У квадрата все стороны равны . В данном квадрате имеется биссектриса(AC). Поэтому получается 2 треугольника (АВС и АСD) . DC и AD катеты треугольника ( ACD ) . АВ и АС катеты треугольника АВС. АВ расположен напротив катета DC . AD расположен напротив катета BC . Из этого можно вынести что AD||BC и AB||DC.
Похожие вопросы
Предмет: Русский язык,
автор: 65798
Предмет: Английский язык,
автор: ordabay
Предмет: Русский язык,
автор: эдиТОЧка
Предмет: Литература,
автор: SeliCh
Предмет: Математика,
автор: elviart