Предмет: Алгебра,
автор: 00Smith
Алгебра 10 класс
24 балла
Приложения:
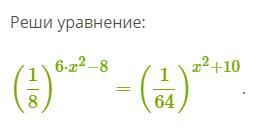
Ответы
Автор ответа:
0
Ответ: во вложении Объяснение:
Приложения:
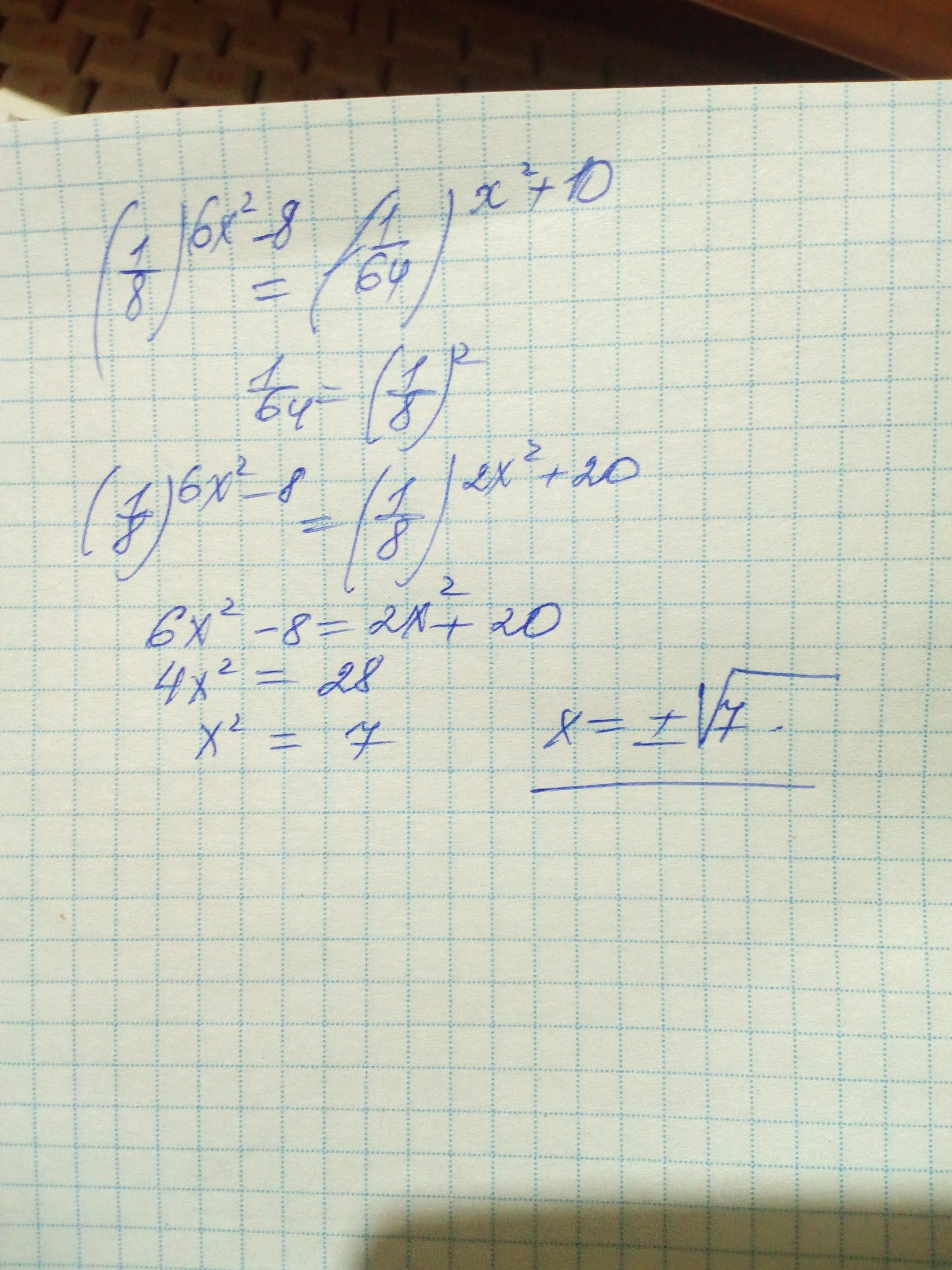
Автор ответа:
1
Согласно закону , имеем:
Основания степеней равны, значит, равны их показатели:
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: aa1ss2
Предмет: Другие предметы,
автор: irinika77
Предмет: Русский язык,
автор: H37
Предмет: Математика,
автор: Нарминаша
Предмет: Математика,
автор: 3Фатима111111111