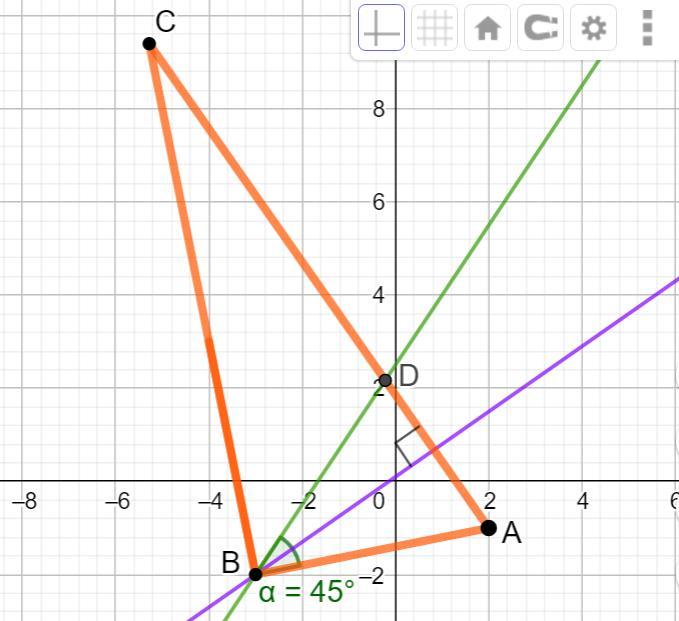
Составьте уравнение сторон треугольника ABC, зная одну его вершину A(2;-1), а также уравнения высоты 7x-10y+1=0 и биссектрисы 3x-2y+5=0, проведённых из одной вершины.
Ответы
Находим координаты точки В как точки пересечения высоты и биссектрисы.
7x - 10y + 1 = 0 7x - 10y + 1 = 0
3x - 2y + 5 = 0 (*(-5)) -15x + 10y - 25 = 0
-8x - 24 = 0
x = 24/(-8) = - 3, y = (3*(-3) + 5)/2 = -4/2 = -2.
Точка В(-3; -2). Вектор АВ = (-3-2; -2-(-1)) = (-5; -1)
Получаем уравнение АВ: (х - 2)/(-5) = (у + 1)/(-1) (каноническое).
5у + 5 = х - 2, х - 5у - 7 = 0 (общее)
у = (1/5)х - (7/5) (с угловым коэффициентом).
По коэффициентам общих уравнений стороны АВ и биссектрисы находим угол между ними.
tgα = (A1B2 - A2B1)/(A1A2 + B1B2) = (3*(*5) - 1*(-2))/(3 + 10) = 13/13 = 1.
Это угол 45 градусов.
На такой же угол от биссектрисы будет отстоять сторона ВС треугольника.
Находим угловой коэффициент (тангенс угла наклона к оси Ох) биссектрисы из общего уравнения: к = (3/2).
Тогда угол наклона стороны ВС к оси Ох равен сумме углов с к1 = 1 и к2 = (3/2) = 1,5.
tgβ = (k1 + r2)/(1 - k1k2) = (1 + 1,5) \ (1 - 1*1,5) = 2,5 / (-0,5) = -5.
Тогда уравнение ВС: у = -5х + в.
Дл определения параметра "в" подставим координаты точки В.
-2 = (-5)*(-3) + в, отсюда в = -2 - 15 = -17.
Уравнение ВС: у = -5х - 17.
Уравнение стороны АС находим как прямой, перпендикулярной высоте (с учётом А1А2 + В1В2 = 0) : 10х + 7у + С = 0.
Для определения С подставим координаты точки А:
10*2 + 7*(-1) + С = 0, откуда С = 7 - 20 = -13.
Уравнение АС: 10х + 7у - 13 = 0.