Предмет: Математика,
автор: aleksaaaaaaa86
даю 40 баллов
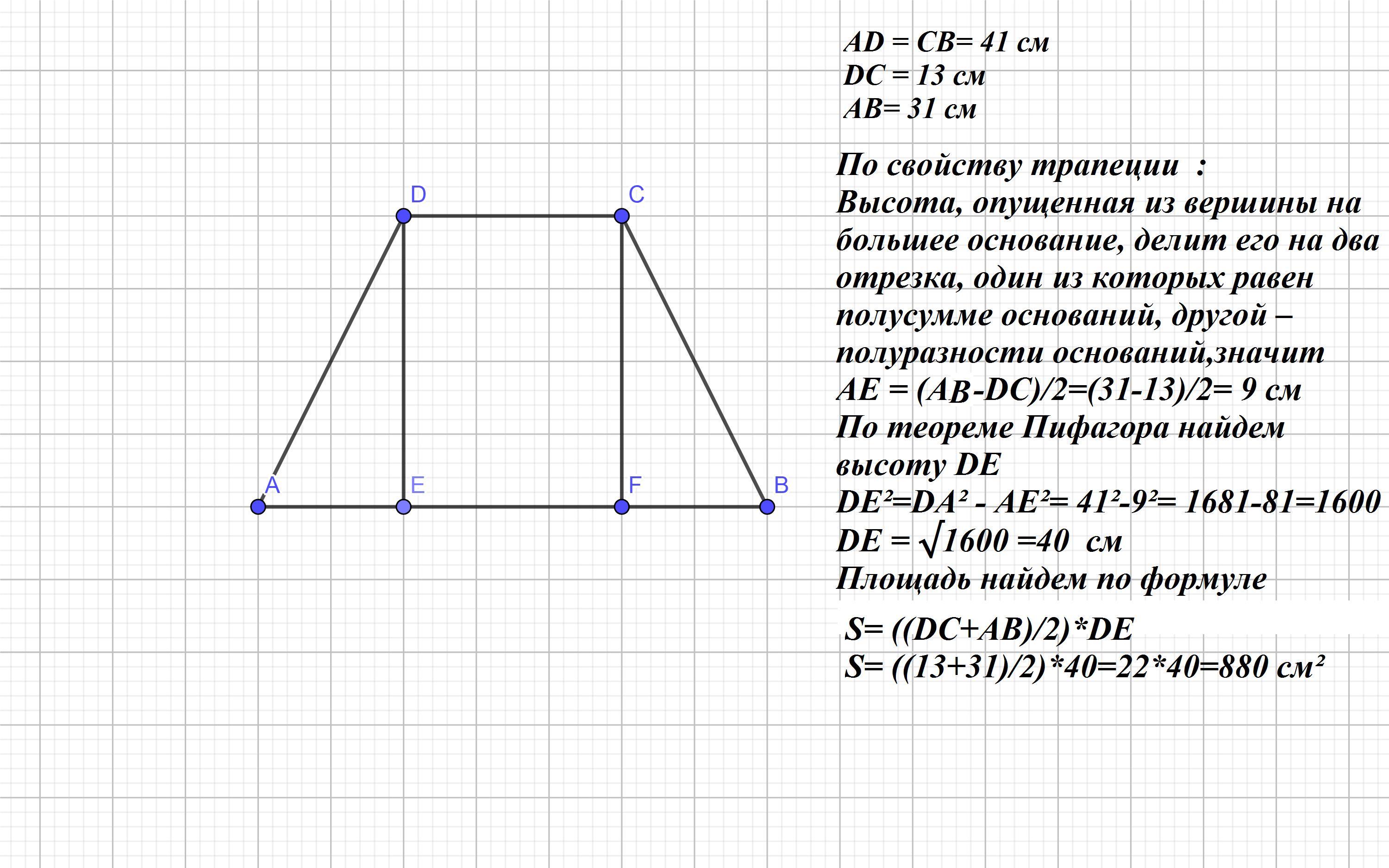
Основания равнобедренной трапеции равны 13 см и 31 см, а боковая сторона 41 см. Найди площадь трапеции .
aleksaaaaaaa86:
нужно пошаговое действие
Ответы
Автор ответа:
4
Ответ:
Пошаговое объяснение:
Площадь равнобедренной трапеции можно узнать по формуле :
S=
по условию :
а= 31 см
b= 13 см
с= 41 см
Второе решение во вложении
Приложения:
b.
Автор ответа:
3
пусть проекция боковой стороны на основание
z = (31-13)/2 = 18/2 = 9 см
и высоту трапеции найдём по теореме Пифагора
41² = z² + h²
1681 = 81 + h²
h² = 1600
h = √1600 = 40 см
Площадь
S = 1/2*(a + b) * h = 1/2*(13+31)*40 = 44 * 20 = 880 см²
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Английский язык,
автор: ann5171
Предмет: Русский язык,
автор: punin98
Предмет: Математика,
автор: Bagirara
Предмет: Математика,
автор: матиматик20