Question

Помогите!!! Решите неравенство sin x < cos x .
правильный ответ:
2πl + 5π/4 < x < 9π/4 + 2πl , l ∈ Z
как его получили объясните пожалуйста понятно

Answer 1

Поступим следующим образом: косинус перенесем влево с противоположным знаком и обе части разделим на $\sqrt{2}$(это же самое, что умножить на дробь $\frac{1}{\sqrt2}$) Имеем:

$\sin x-\cos x<0\\\\\frac{1}{\sqrt2}\cdot \sin x-\frac{1}{\sqrt2}\cos x <0$

Заметим, что

$\frac{1}{\sqrt2}=\cos\frac{\pi}{4}=\sin \frac{\pi}{4}$

Если переписать неравенство в следующем виде -

$\cos\frac{\pi}{4}\sin x-\sin \frac{\pi}{4}\cos x<0$,

то легко можно заметить в левой части формулу синуса разности аргументов. Окончательно имеем:

$\sin(x-\frac{\pi}{4})<0$

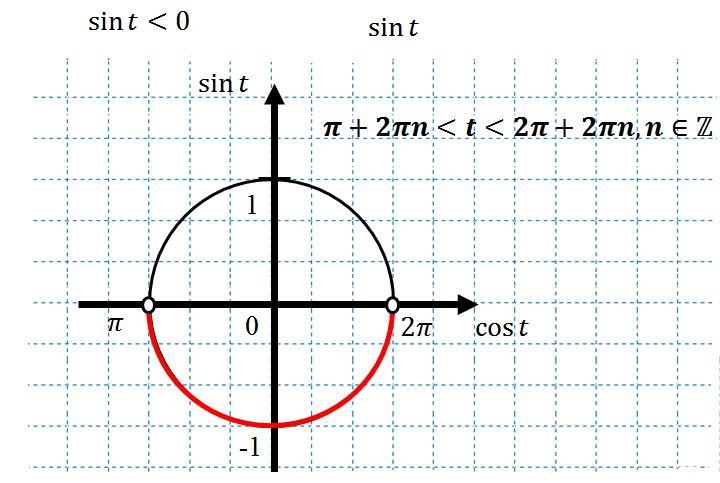
Сделаем замену: $x-\frac{\pi}{4}=t$. Таким образом мы свели исходное неравенство к наипростейшему вида $\sin t <0$. Решим его при помощи числовой окружности (вложение). Окончательно имеем:  $\pi+2\pi n<t<2\pi+2\pi n, n\in \mathbb Z$. Возвращаемся к обратной замене: $\pi+2\pi n<x-\frac{\pi}{4} <2\pi+2\pi n, n\in \mathbb Z$.

Ко всем 3-ем частям неравенства прибавляем $\frac{\pi }{4}$ и получаем окончательный ответ:   $\frac{5\pi}{4} +2\pi n<x <\frac{9\pi}{4} +2\pi n, n\in \mathbb Z$

ОТВЕТ: $\frac{5\pi}{4} +2\pi n<x <\frac{9\pi}{4} +2\pi n, n\in \mathbb Z$.