Question

Помогите!!! Решите неравенство sin x < cos x .
правильный ответ:
2πl + 5π/4 < x < 9π/4 + 2πl , l ∈ Z
как его получили объясните пожалуйста понятно

Answer 1

$sinx-cosx < 0$

$cosx=sin(\frac{\pi }{2} -x)$

$sinx- sin(\frac{\pi}{2} -x)<0$

$2sin\frac{x-(\frac{\pi }{2}- x) }{2} \cdot cos \frac{x+(\frac{\pi }{2}- x) }{2}<0\\ \\ 2sin(x-\frac{\pi }{4} )\cdot cos\frac{\pi }{4}<0\\ \\ sin(x-\frac{\pi }{4} ) <0\\\\-\pi+2\pi k <x-\frac{\pi }{4}<2\pi k, k \in Z\\\\-\pi+\frac{\pi }{4}+2\pi k <x< \frac{\pi }{4}+2\pi k, k \in Z\\\\-\frac{3\pi }{4}+2\pi k <x< \frac{\pi }{4}+2\pi k, k \in Z$

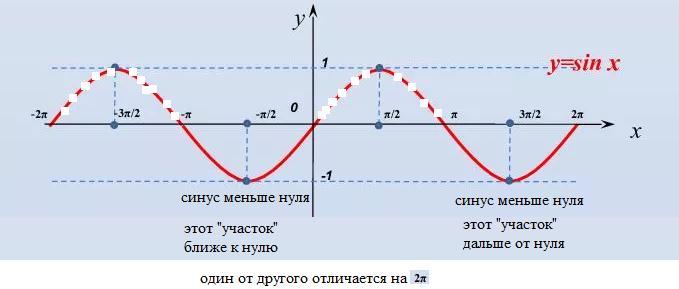
Этот промежуток ближе к нулю, чем тот, который в ответе.

Чтобы получить тот, который в ответе, надо прибавить 2π

$-\frac{3\pi }{4}+2\pi+2\pi k <x< \frac{\pi }{4}+2\pi+2\pi k, k \in Z\\ \\ \frac{5\pi }{4}+2\pi k <x< \frac{9\pi }{4}+2\pi k, k \in Z$

Или в процессе решения неравенства брать промежуток, который дальше от нуля справа ( см. рис):

$sin(x-\frac{\pi }{4} ) <0\\\\\pi+2\pi k <x-\frac{\pi }{4}<2\pi+2\pi k, k \in Z\\\\\pi+\frac{\pi }{4}+2\pi k <x<2\pi+ \frac{\pi }{4}+2\pi k, k \in Z\\\\\frac{5\pi }{4}+2\pi k <x< \frac{9\pi }{4}+2\pi k, k \in Z$