Предмет: Алгебра,
автор: Fakla
Решить показательное неравенство:
Приложения:
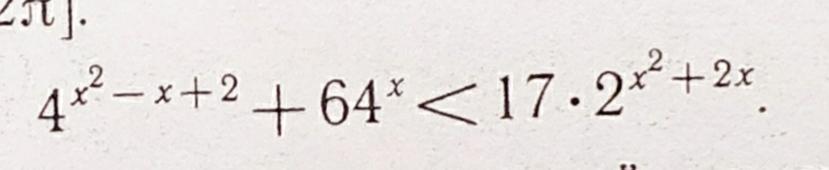
Ответы
Автор ответа:
1
Сделаем замену :
+ - +
______₀_______₀______
1/16 1
/////////////////
m ∈ (1/16 ; 1)
Похожие вопросы
Предмет: Українська мова,
автор: Улька1107
Предмет: Русский язык,
автор: Катерина01
Предмет: Українська мова,
автор: oroszeva
Предмет: Биология,
автор: dasha1460
Предмет: Математика,
автор: елиза194202