Предмет: Алгебра,
автор: Anapheron2
для каждого значения а найдите область определения функции
Приложения:
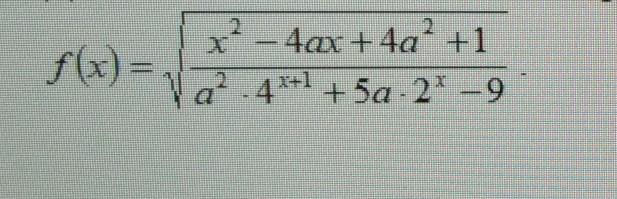
Ответы
Автор ответа:
0
Так как (x-2a)²≥0 при любых а и х, то (x-2a)²+1>0
Осталось решить неравенство:
Решаем методом интервалов:
Ясно, что либо ,
тогда a >0 и
и решением неравенства является:
либо, тогда
О т в е т.
при a >0
при a < 0
Похожие вопросы
Предмет: Русский язык,
автор: keenys
Предмет: Русский язык,
автор: lera39
Предмет: Английский язык,
автор: Кристюшка8464
Предмет: Музыка,
автор: Risha0802
Предмет: Математика,
автор: miotelko98