Question

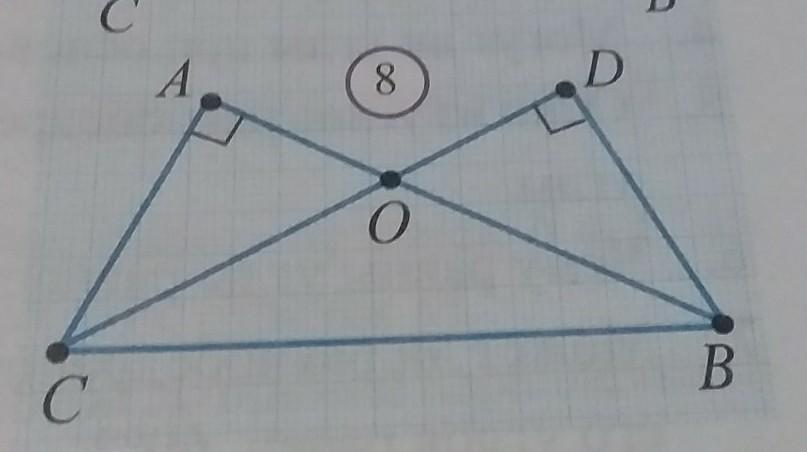
Будут ли равны треугольники BAC и CDB, если на рисунке 8:a)AC=BD; b) OA=OD; c) <OCB=<OBC; g) BC=OD; h)<ACB=<DBC​

Answer 1

ΔBAC и ΔCDB являются прямоугольными.

Признаки равенства прямоугольных треугольников:

• по двум катетам;

• по катету и прилежащему к нему углу;

• по гипотенузе и острому углу;

• по гипотенузе и катету.

а)

АС = DB по условию.

ВС — общая сторона.

Значит, ΔBAC = ΔCDB по гипотенузе и катету.

b)

Рассмотрим ΔАОС и ΔDOB.

OA=OD по условию.

∠АОС = ∠DOB, как вертикальные.

Значит, ΔАОС = ΔDOB по катету и прилежащему к нему углу.

У равных треугольников равны соответствующие элементы.

Отсюда, AC = DB.

ВС — общая сторона.

Значит, ΔBAC = ΔCDB по гипотенузе и катету.

c)

∠OCB = ∠OBC по условию.

Значит, ΔOCB равнобедренный и ОС = ОВ.

∠АОС = ∠DOB, как вертикальные.

Значит, ΔАОС = ΔDOB по гипотенузе и острому углу.

У равных треугольников равны соответствующие элементы.

Отсюда, AC = DB.

ВС — общая сторона.

Значит, ΔBAC = ΔCDB по гипотенузе и катету.

g)

Не будут равны.

h)

∠ACB = ∠DBC​ по условию.

ВС — общая сторона.

Значит, ΔBAC = ΔCDB по гипотенузе и острому углу.

Ответ:

а) будут равны;

b) будут равны;

c) будут равны;

g) не будут равны;

h) будут равны.