Предмет: Алгебра,
автор: danniekot
Пожалуйста срочно найдите первообразную (интегрирование по частям)
(3x + 7)cos5xdx
Ответы
Автор ответа:
1
Найдем первообразную для функции в виде неопределенного интеграла:
Если подынтегральная функция может быть представлена в виде произведения двух непрерывных функций, то справедлива следующая формула:
Предполагается, что нахождение интеграла проще, чем
Таким образом, сделаем соответствующие замены:
(константу
опускаем)
Имеем:
Упрощаем:
Следовательно,
Ответ:
Автор ответа:
1
Ответ:
Вроде как-то так
Объяснение:
Приложения:
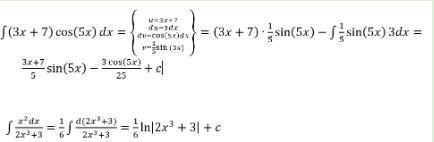
Похожие вопросы
Предмет: Русский язык,
автор: olya1233
Предмет: Русский язык,
автор: Dilarka
Предмет: Английский язык,
автор: Danil121
Предмет: Математика,
автор: айнур110