Question

Помогите!!! Решите неравенство sin x < cos x .

Answer 1

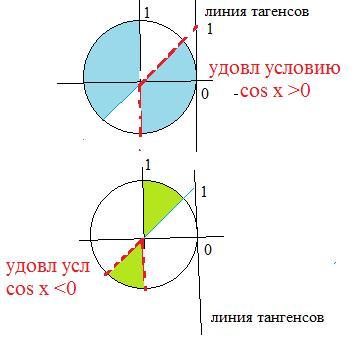
Eсли cosx > 0, т. е х в 1 и 4 четверти, делим на cosx

tgx < 1⇒  -(π/2)+πk < x < (π/4)+πk, k∈Z

Неравенству удовлетворяют корни, для которых соsx>0

Получаем

-(π/2)+2·πk < x < (π/4)+2·πk, k∈Z

Eсли cosx < 0, т. е х в 2 и 3 четверти, делим на cosx

tgx >  1⇒  (π/4)+πn < x < (π/2)+πn, n∈Z

Неравенству удовлетворяю корни, для которых соsx>0

Получаем

(3π/4)+2·πn < x < (π/2)+2·πn, n∈Z

О т в е т. Объединение ответов:

((π/2)+2·πk ; (π/4)+2·πk) U (3π/4)+2·πn ; (π/2)+2·πn), k, n∈Z