Question

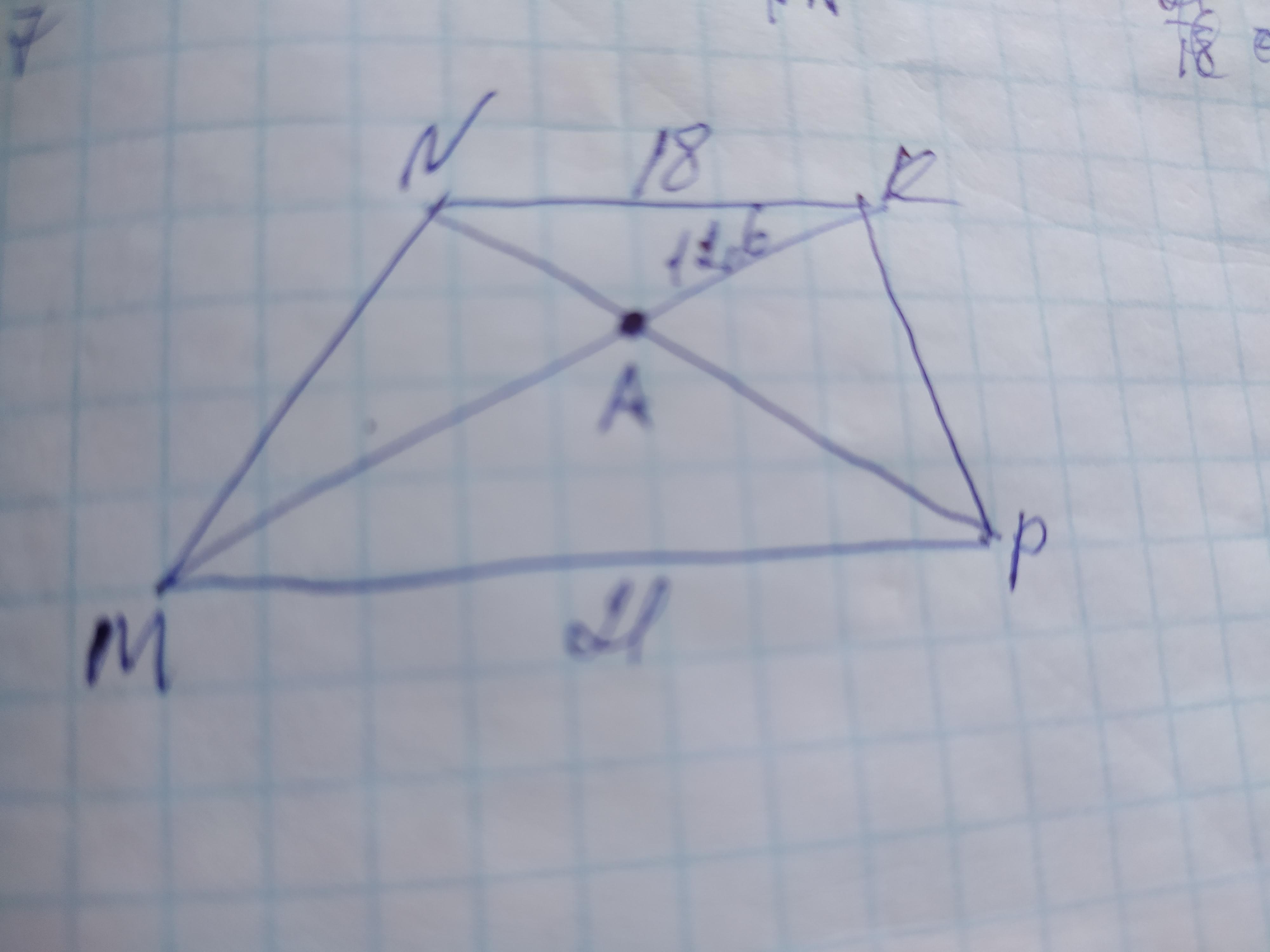
Четырёхугольник MNKP - трапеция (NK//MP) A - точка пересечения диагоналей. Найдите MA и MK, если NK = 18 см, MP = 21 см, AK = 12,6 см.​

Answer 1

Ответ: МК=27,3см, МА=14,7см

Объяснение: диагонали трапеции делят её на 2 пары подобных треугольника:

∆МАР подобен ∆NKA, поэтому

МР/NK=MA/AK. Пусть МА=х, тогда:

21/18=х/12,6

18х=21×12,6

18х=264,6

х=264,6÷18=14,7

МА=14,7см

Тогда МК=МА+АК=14,7+12,6=27,3см