Предмет: Алгебра,
автор: bertain
100 б + лучший ответ. Задание на фотографиях
Приложения:

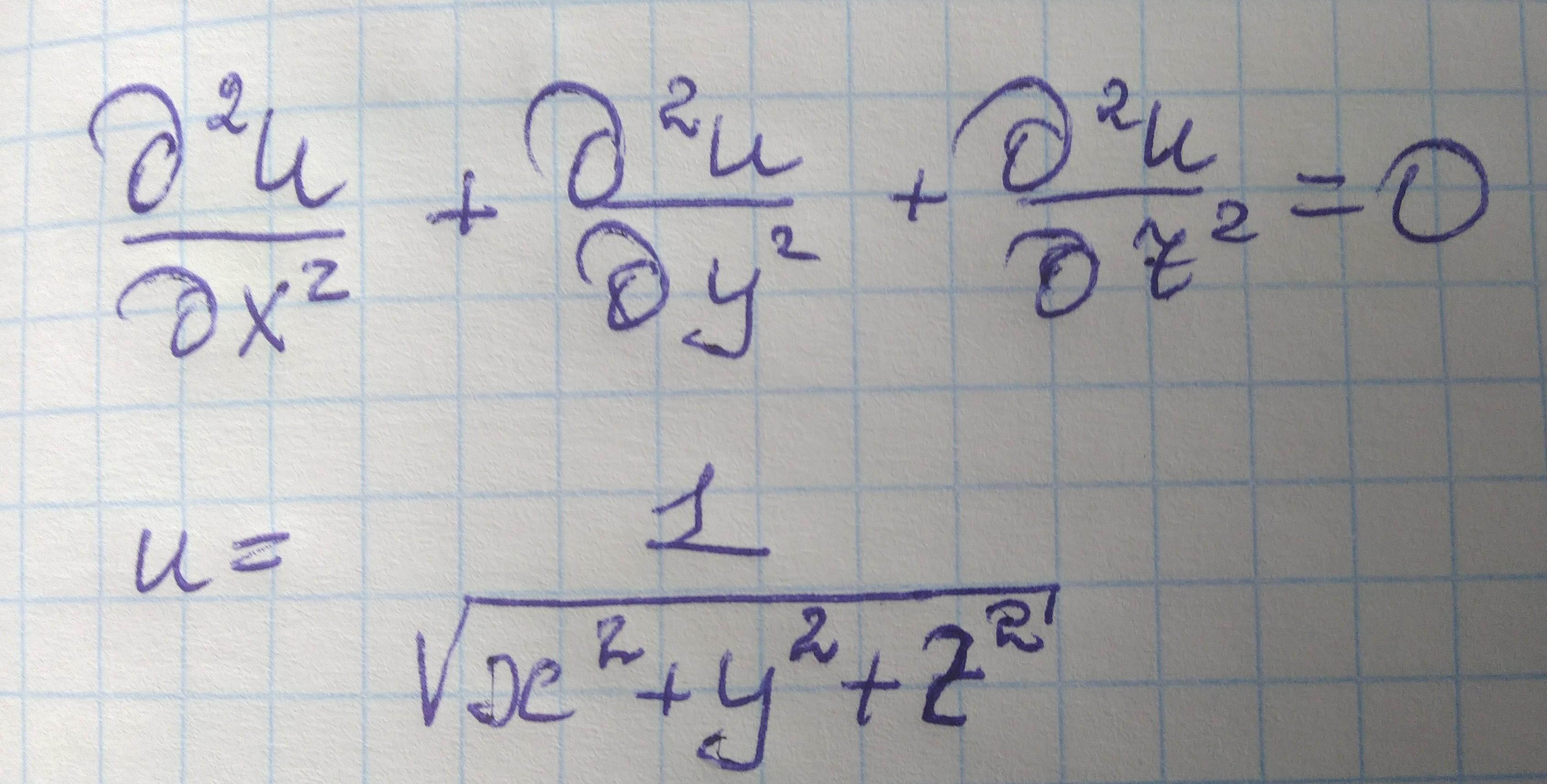
Ответы
Автор ответа:
3
Заданная функция удовлетворяет данному уравнению.
IrkaShevko:
у вас как-то второго порядка производные частные не правильные
Магистр можешь помочь?
Автор ответа:
3
Ответ:
Удовлетворяет
Объяснение:
Приложения:
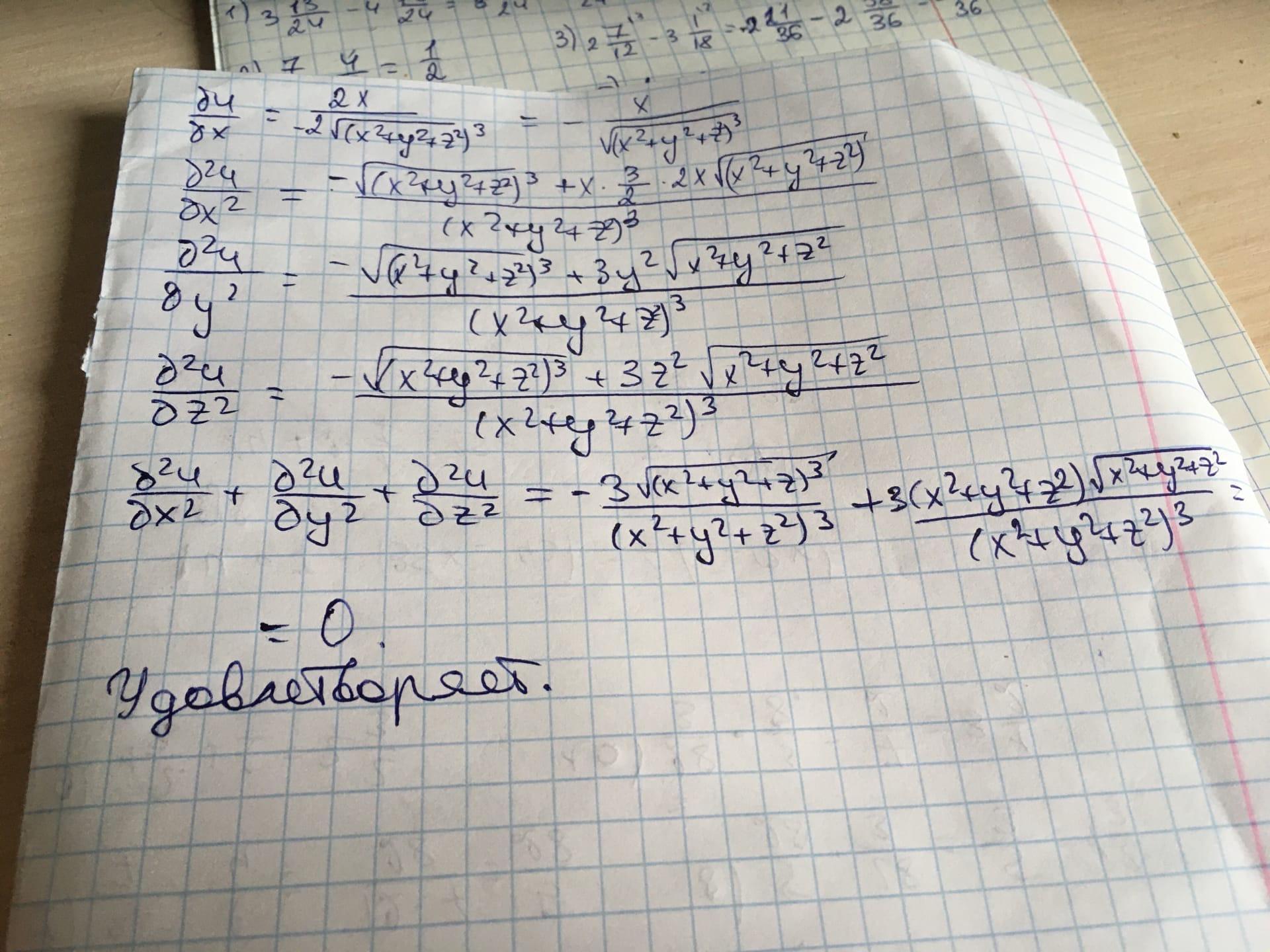
надеюсь понятно, если что спрашивайте
Похожие вопросы
Предмет: Русский язык,
автор: TepMuHaToP
Предмет: Другие предметы,
автор: Ulyashka
Предмет: Другие предметы,
автор: ЛутИк
Предмет: Математика,
автор: wwwwwssss2324
Предмет: География,
автор: Задание2004