Предмет: Алгебра,
автор: danilpedora58
Помогите решить там 4 не полных квадратных уравнивания
Приложения:
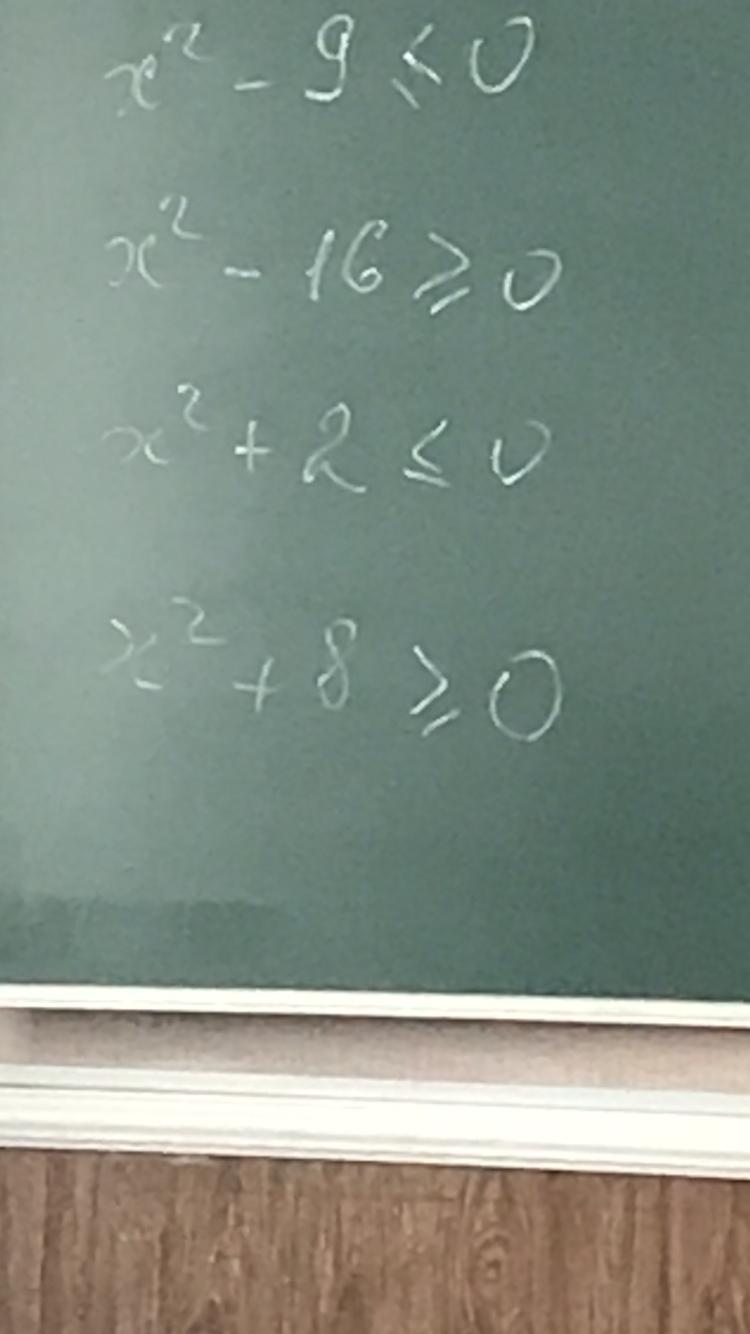
Ответы
Автор ответа:
1
Ответ:
1)Х-9<0
х+9<0
х=10
х=10:2
х=5
(вроде так)
Объяснение:
перед х есть цифра один его прибовляем и получаем 10, 10:2 там уже понятно
Paytonmoormeir:
1)x2−9≤0,(x−3)(x+3)≤0x∈[−3;3]2)x2−16≥0,(x−4)(x+4)≥0x∈(−∞,−4]∪[4,+∞)3)x2+2≤0⇒x∈∅,takkak(x2+2)≥24)x2+8≥0⇒x∈(−∞,+∞),takkak(x2+8)≥8
вот это правильно
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: Денис123123123
Предмет: Русский язык,
автор: ДинараН
Предмет: Русский язык,
автор: Масья
Предмет: Биология,
автор: karina021129201
Предмет: Алгебра,
автор: Kukamo