Предмет: Математика,
автор: ypuziny
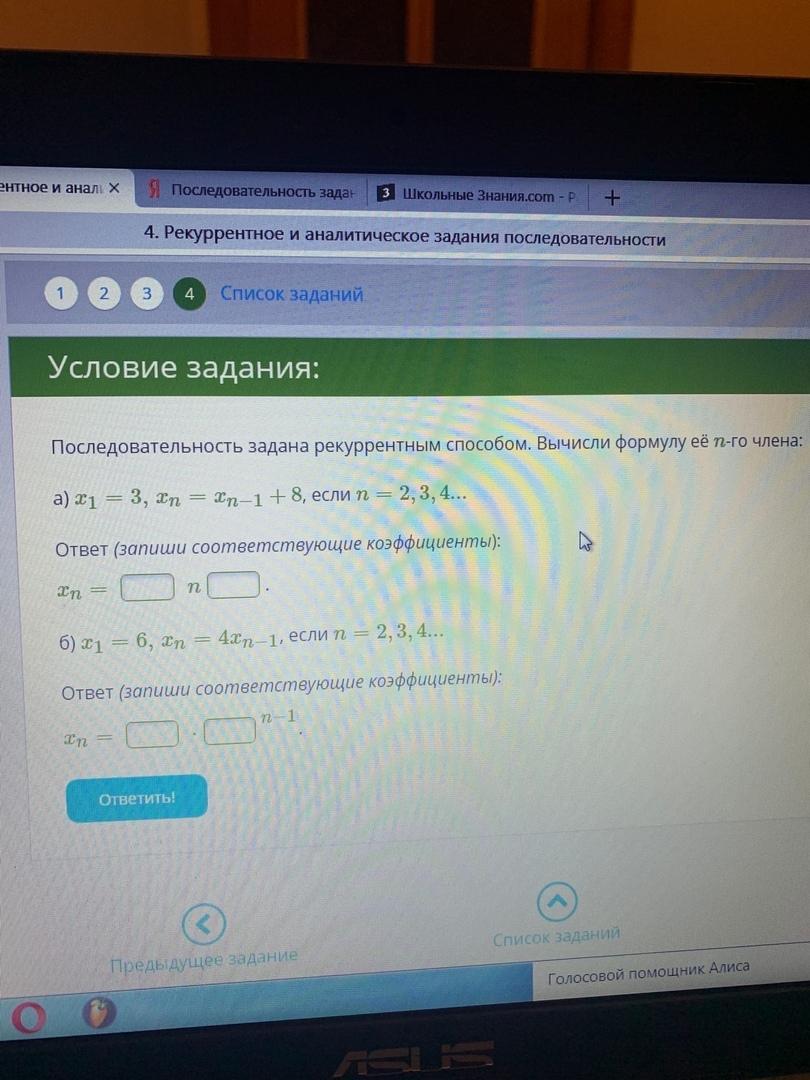
Последовательность задана рекуррентным способом. Вычисли формулу её n-го члена:
а) x1=3,xn=xn−1+8, если n=2,3,4...
Ответ (запиши соответствующие коэффициенты):
xn=
n
.
б) x1=6,xn=4xn−1, если n=2,3,4...
Ответ (запиши соответствующие коэффициенты):
xn=
⋅
n−1.
Приложения:
Ответы
Автор ответа:
59
Пошаговое объяснение:
а) x₁=3, xₙ=xₙ₋₁+8, если n=2,3,4...
х₂=х₁+8=3+8=11, d=х₂-х₁=11-3=8
хₙ=х₁+d(n-1) , хₙ=3+8(n-1) , хₙ=8n-5.
б) x₁=6,xₙ=4xₙ₋₁, если n=2,3,4...
х₂=4*х₁=4*6=24 ,q=х₂:х₁=24:6=4.
хₙ=х₁*qⁿ⁻¹ , хₙ=6*4ⁿ⁻¹
Похожие вопросы
Предмет: Русский язык,
автор: Найтири
Предмет: Русский язык,
автор: 260501nik
Предмет: Русский язык,
автор: Nadya545
Предмет: Алгебра,
автор: Vero1234
Предмет: Химия,
автор: furma1