Предмет: Математика,
автор: anastasiya343332
Вычислить подробно интеграл
Приложения:
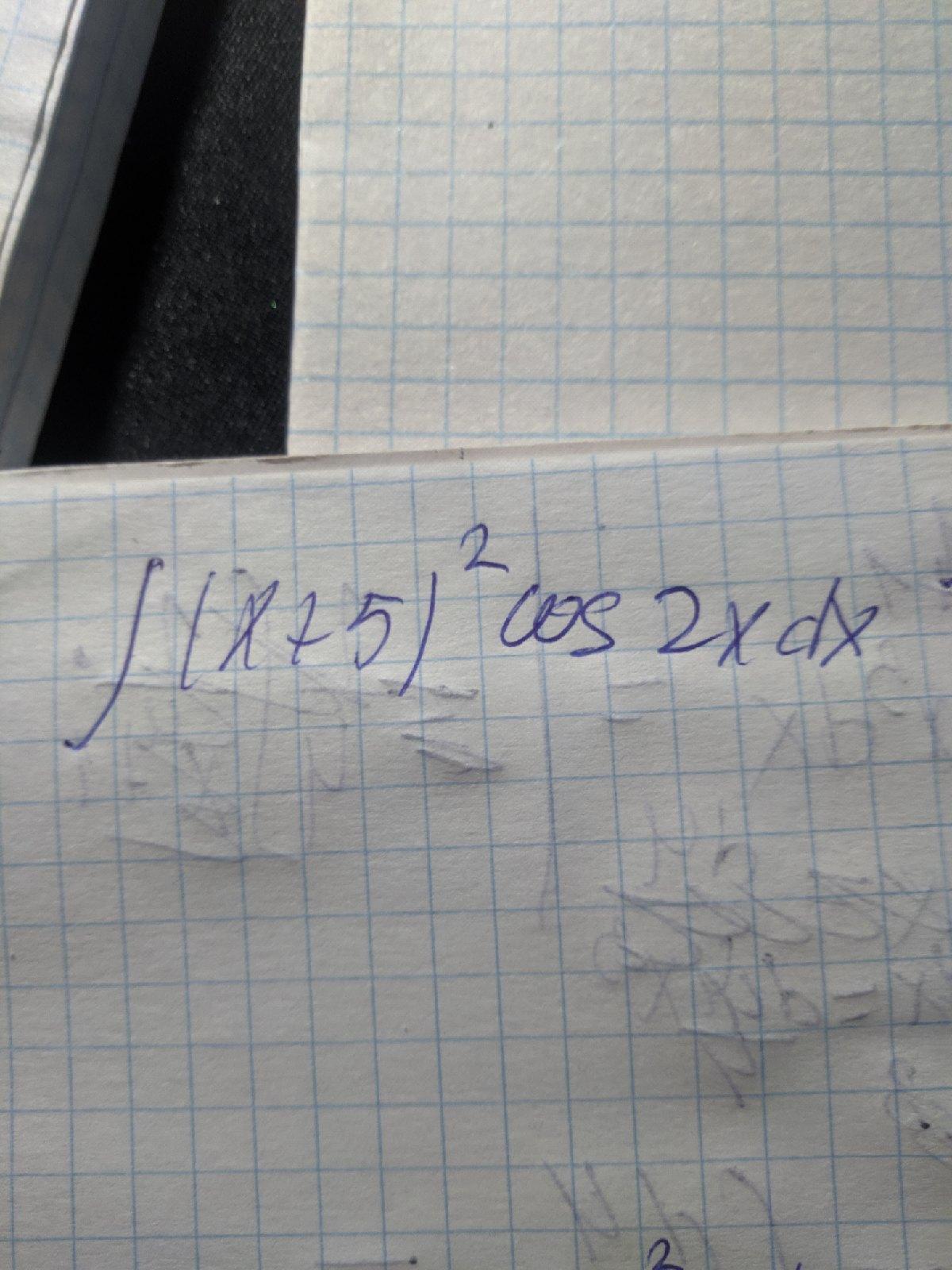
Ответы
Автор ответа:
1
Если подынтегральная функция может быть представлена в виде произведения двух непрерывных функций, то справедлива следующая формула для неопределенного интеграла, которая называется интегрированием по частям:
Вычислим неопределенный интеграл
Сделаем соответствующую замену:
Пусть , тогда
, а
, тогда
(константу
опускаем).
Получаем:
Сделаем еще одну соответствующую замену:
Пусть , тогда
, а
, тогда
(константу
опускаем).
Получаем:
Вычисляем:
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Ruslan71
Предмет: Русский язык,
автор: TaTaRiNiN
Предмет: Українська мова,
автор: Tanithka1
Предмет: Биология,
автор: pichkurova561
Предмет: Математика,
автор: WOTZADAЧA