Предмет: Математика,
автор: mashakinder20001
вычислить интеграл подробно
Приложения:
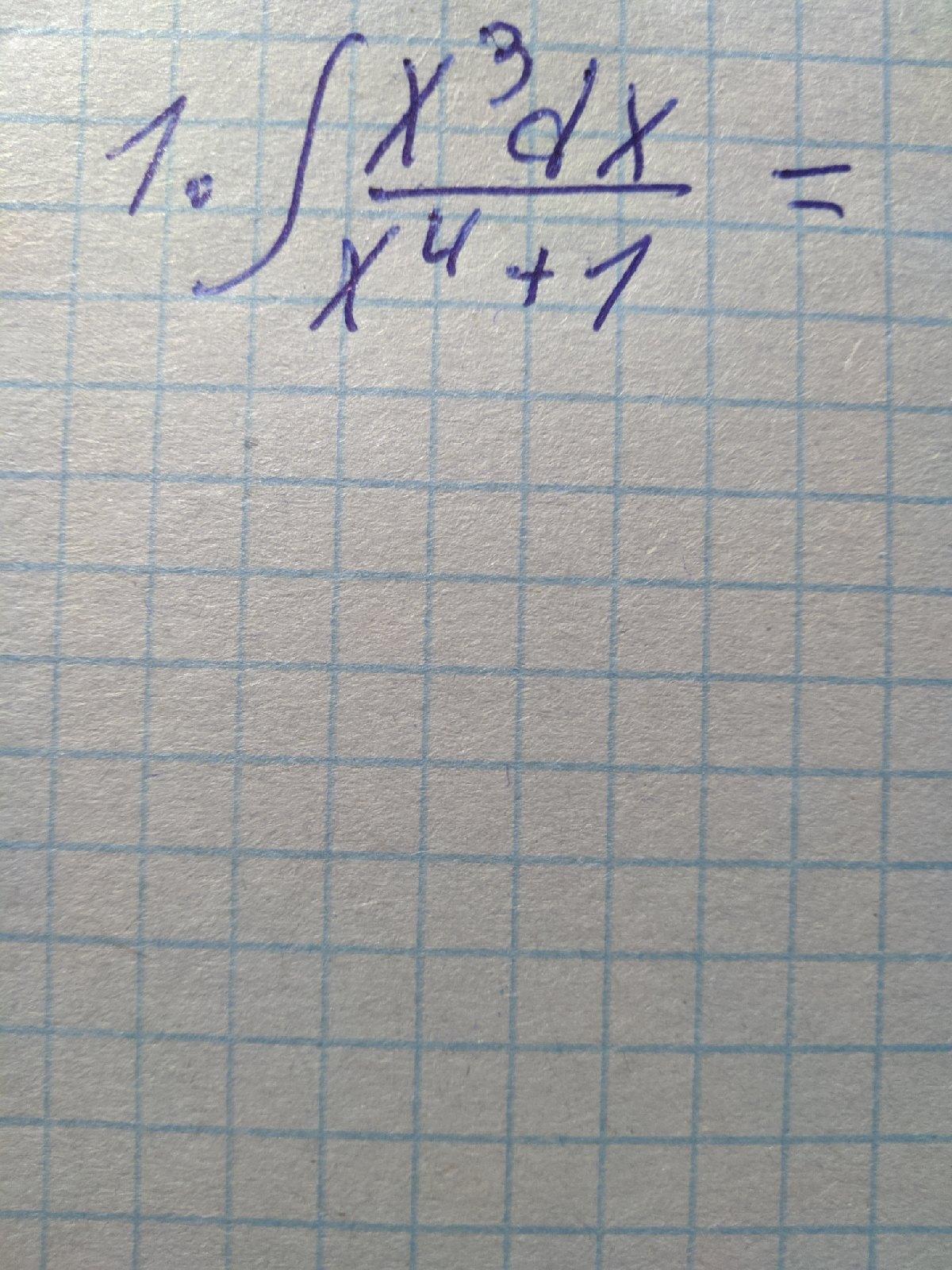
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Автор ответа:
0
Ответ: во вложении Пошаговое объяснение:
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: Alekseevna7
Предмет: Английский язык,
автор: Наташа19999
Предмет: Русский язык,
автор: 375297758796
Предмет: История,
автор: AdinaAdina1