Question

большая диагональ ромба равна 12√3 а один из углов равен 120 найти меньшую диагональ

Answer 1

Ответ:

12

Объяснение:

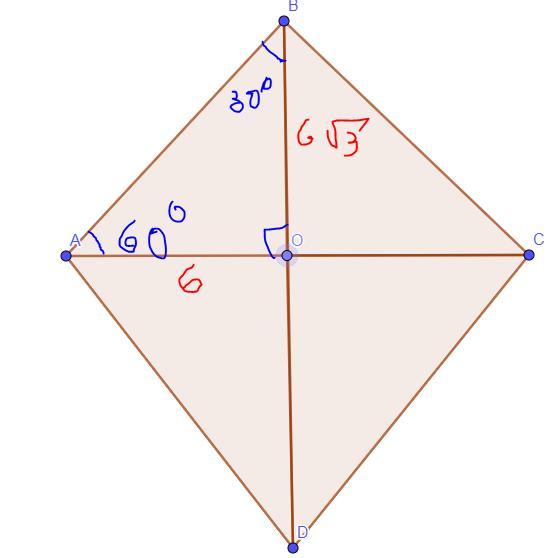
BD - наибольшая диагональ = 12√3.

<A = 120.

1) Посколько диагонали ромба одновременно перпедикулярны (т.е. создают 4 угла по 90°) и являются биссектрисами углов, то меньшая биссектриса AC разбивает <A на 60°.

Из треугольника ABO, нам известно, что <O = 90°. Не сложно найти тогда и <B:

$<B = 180 - (60+90) = 30$ °.

2) DB = 2OB, посколько диагонали ромба точкой сечения делятся пополам, т.е OB = 6√3

Из треугольника ABO найдём сторону AO, лично мне будет удобно использовать теорему синусов, кто-то может использовать тригонометрические соотношения углов, как вам удобно. Итак, имеем:

$\frac{AO}{sin30} = \frac{OB}{sin60} ;\\\frac{AO}{\frac{1}{2}} = \frac{6\sqrt{3} }{\frac{1}{2} } ;\\12 = 2AO;\\AO = 6.$

3) AC = 2AO, посколько диагонали ромба точкой сечения делятся пополам, т.е:

$AC = 2 * 6 = 12$ - значения наименьшей диагонали.