Question

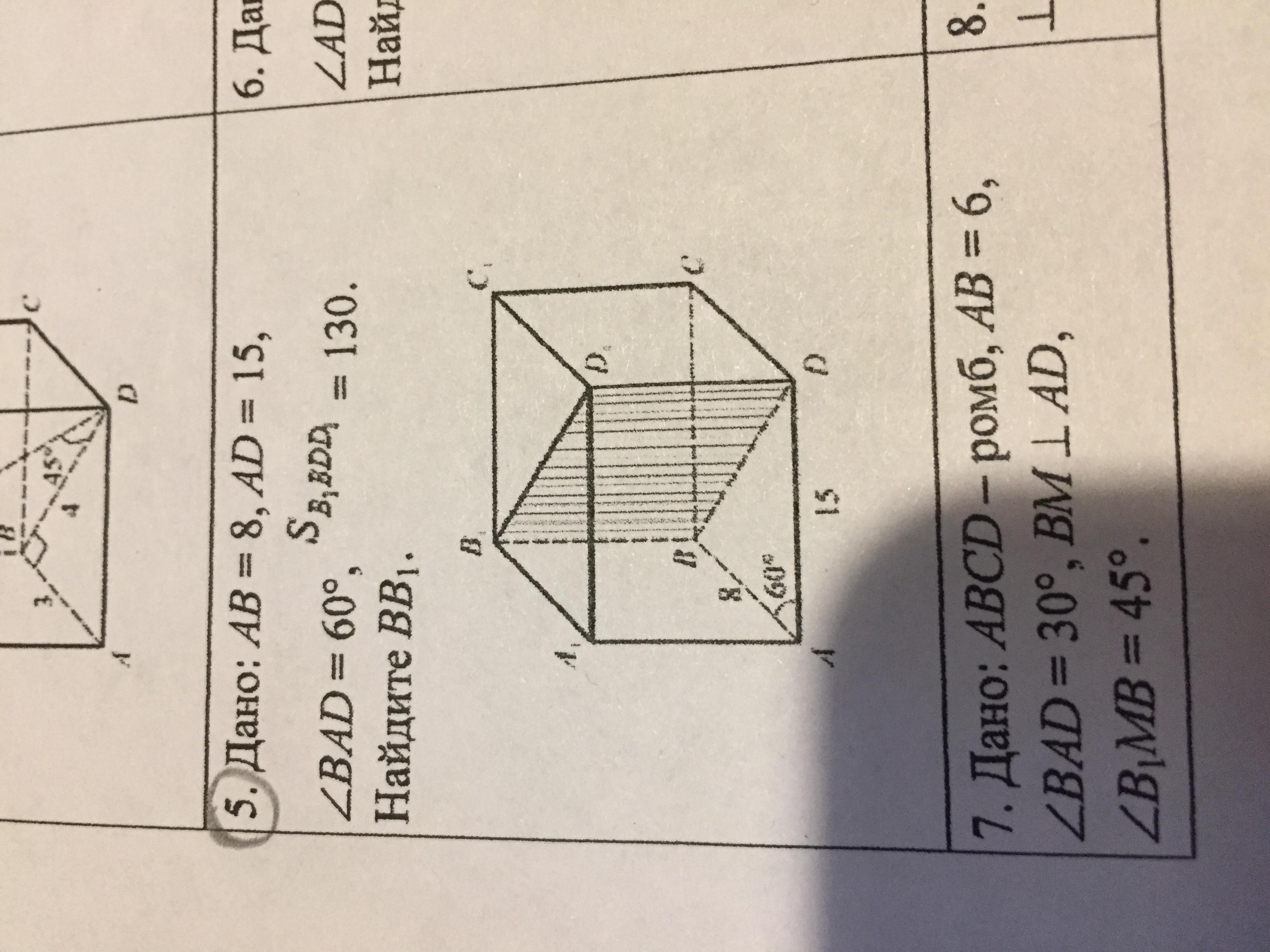
Помогите, пожалуйста, решить 5 задачу

Answer 1

Ответ:

BB₁ = 10.

Объяснение:

Итак, мы имеем дело с призмой и диагональным сечением. Но к этому чуть-чуть позже.

1) Согласно теореме косинусов, из треугольника ABD:

$BD = \sqrt{AB^{2} + AD^{2} -2*AB*AD*cos(60)}$, подставим известные нам значения в формулу:

$BD = \sqrt{8^{2} +15^{2} - 2 * 8*15*\frac{1}{2} } = \sqrt{64+225-8*15} = \sqrt{64+125-120} = \sqrt{169} = 13.$

2) При пересечении призмы диагональной плоскостю, сечение представляет собой параллелограмм. В даном случае параллелограмм это B₁BDD₁. Напомним формулу паралеллограма:

$S = a*h$, где a - основание, h - высота.

Так как высота совпадает с боковой стороной, то вместо h выступает BB₁, а основание a - BD. Нам известно, что площадь сечения равна 130, BD - мы нашли, подставим значения в формулу и выразим оттуда BB₁:

$S = BD*BB1; 130 = 13 * BB1; BB1 = \frac{130}{13} = 10$ см.