Предмет: Алгебра,
автор: Andrey21vek
даю 90 баллов!!!!решите примеры заранее спасибо)
Приложения:
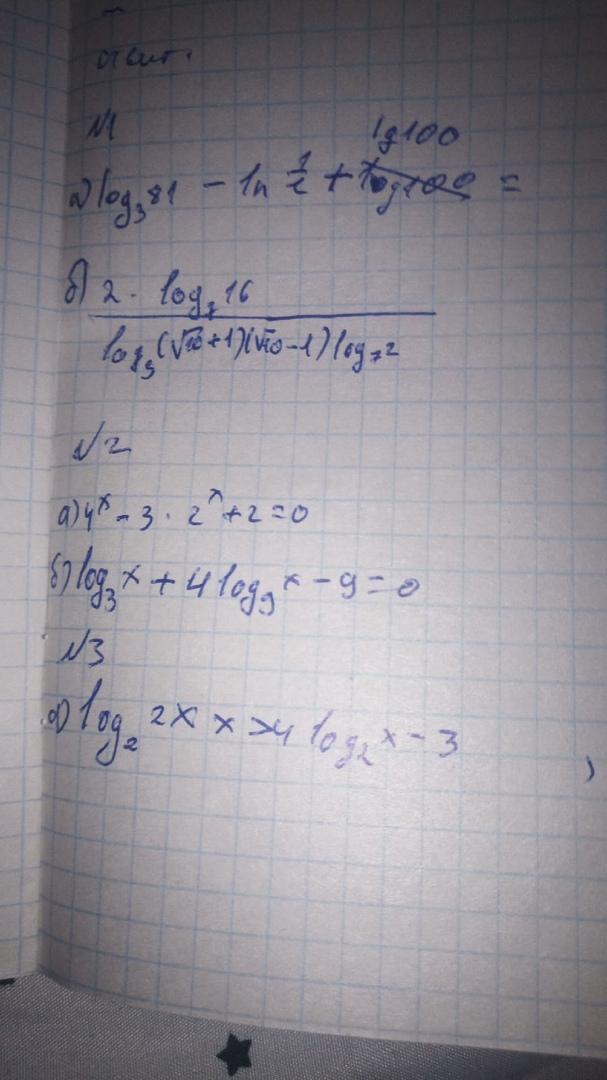
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: Emeraldgirl
Предмет: Русский язык,
автор: MashaDanova
Предмет: Русский язык,
автор: Bonbon820
Предмет: Математика,
автор: nadaryanmher
Предмет: Обществознание,
автор: frolovakristin